Scattered order

This article is about order theory. For the Australian post-punk band, see Scattered Order.

In mathematical order theory, a scattered order is a linear order that contains no densely ordered subset with more than one element (Harzheim 2005:193ff.)

A characterization due to Hausdorff states that the class of all scattered orders is the smallest class of linear orders which contains the singleton orders and is closed under well-ordered and reverse well-ordered sums.

Laver's theorem (generalizing Fraïssé's conjecture) states that the embedding relation on the class of countable unions of scattered orders is a well-quasi-order (Harzheim 2005:265).

The order topology of a scattered order is scattered. The converse implication does not hold, as witnessed by the lexicographic order on 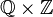$\mathbb Q\times\mathbb Z$ .

References

Egbert Harzheim (2005). Ordered Sets. Springer. ISBN 0-387-24219-8.
Laver, Richard (1971). "On Fraïssé's order type conjecture". Annals of Mathematics 93 (1): 89–111. doi:10.2307/1970754. JSTOR 1970754.