Scale relativity

Scale relativity is a theory of space-time initially developed by Laurent Nottale, researcher at Paris Observatory, near Paris. It is an extension of the concept of relativity found in special relativity and general relativity to physical scales (time, length, energy, or momentum scales). Nottale's theory starts with a continuous space in which differentiability is not assumed and uses fractal geometry and the principle of scale relativity to obtain quantum laws. Scale relativity means that scales always depend on the scale used as a reference. As a consequence, the fundamental laws of physics cannot involve scales themselves because their values are arbitrary choices. The geometry of space itself becomes scale dependent by relaxing the hypothesis of differentiability. While differentiable trajectories found in standard physics are automatically scale invariant, it is the main insight of the theory that also certain non-differentiable trajectories (which explicitly depend on the scale of the observer) can be scale invariant and new mathematical tools are developed to model such trajectories.Scale invariance is closely related to the self-similarity observed in fractals. One of the claimed successes of the theory is that the laws of quantum mechanics, like the Schroedinger equation, can be derived directly from a continuous space in which coordinate curves are generally non-differentiable through the use of a new complex total derivative with respect to time in the Euler–Lagrange equation. The mass involved in these laws is of pure geometrical origin and no particle is assumed to derive them.^[1]

Dropping the hypothesis of space differentiability

Scientific theories usually do not improve by adding complexity, but rather by starting from a more and more simple basis. This fact can be observed throughout the history of science. The reason is that starting from a less constrained basis provides more freedom and therefore allows richer phenomena to be included in the scope of the theory. Therefore, new theories usually do not contradict the old ones, but widen their domain of validity and include previous knowledge as special cases. For example, releasing the constraint of rigidity of space led Einstein to derive his theory of general relativity and to understand gravitation. As expected, this theory naturally includes Newton's theory, which is recovered as a linear approximation at small scales.

The same type of approach has been followed by Nottale to build the theory of scale relativity. The basis of current theories is a continuous and two-times differentiable space. Space is by definition a continuum, but the assumption of differentiability is not supported by any fundamental reason. It is usually assumed only because it is observed that the first two derivatives of position with respect to time are needed to describe motion. Nottale's theory is rooted in the idea that differentiability can be abandoned and that this allows quantum laws to be derived.

In terms of geometry, differentiability means that a curve is sufficiently smooth and can be approximated by a tangent. Mathematically, two points are placed on this curve and one observes the slope of the straight line joining them as they become closer and closer. If the curve is smooth enough, this process converges (almost) everywhere and the curve is said to be differentiable. It is often believed that this property is common in nature. However, most natural objects have instead a very rough surface, or contour. For example the bark of trees and snowflakes have a detailed structure that does not become smoother when the scale is refined. For such curves, the slope of the tangent fluctuates endlessly or diverges. The derivative is then undefined (almost) everywhere and the curve is said to be nondifferentiable.

Therefore, when the assumption of space differentiability is abandoned, there is an additional degree of freedom that allows the geometry of space to be extremely rough. The difficulty in this approach is that a new mathematical tools are needed to model this geometry because the classical derivative cannot be used. Nottale found a solution to this problem by using the fact that nondifferentiability implies scale dependence and therefore the use of fractal geometry. Scale dependence means that the distances on a nondifferentiable curve depend on the scale of observation. It is therefore possible to maintain differential calculus provided that the scale at which derivatives are calculated is given, and that their definition includes no limit. It amounts to saying that nondifferentiable curves have a whole set of tangent in one point instead of one, and that there is a specific tangent at each scale.

The proof of space fractality

Nondifferentiability means that the curve has no tangent (see the Von Koch curve for an example of non-differentiable curve). Nottale has shown that the length between any pair of points on a nondifferentiable curve depends on scale and tends toward infinity when the scale is refined, which are the basic properties of fractals. Therefore a continuous space in which differentiability is not assumed is necessarily fractal. The proof uses a contradiction of the Lebesgue's theorem stating that a continuous curve of finite length is differentiable and the fact the absence of tangent implies the absence of straight segments.

Equivalence between matter and space

On the basis of fractal space, Nottale introduces a differential calculus in scale space to take into account scale dependent geometry. This leads to a new "covariant" derivative in the sense that it includes the new fractal geometry. Finally, this new derivative operator can be introduced into the law of motion to derive the laws of quantum mechanics. The mass involved in these equation is not pre-supposed. It is a geometrical integration constant, which means that it arises from the geometry of space. Consequently, particles are a manifestation of space itself.

Galilean scale relativity

Motivating observations

Two everyday observations are, that if we look at an object at a very small distance, say through a microscope, then even the slightest movement of this object will appear very fast; if on the other hand we look up to the sky and follow the movement of a jumbo-jet we sometimes wonder why it doesn't fall down, because from this distance it appears to be almost standing still.
Is this a pure subjective perception? The passengers in the jet will say that the clouds rushing by prove that the plane is moving fast, whereas the earth below is nearly standing still. And if the 'object' under the microscope were an ant that just woke up from coma, it would observe itself moving - relatively to the surface it is bounded to - with merely a few centimeters per minute.
This is reminiscent of the situation where one walks inside a train. One observes oneself walking rather slowly, while an observer outside will add the velocity of the train to the walking speed, and say that the person inside the train is walking fast relatively to the ground. A similar observation led Galileo to formulate a relativity principle of motion. Likewise the former observations led Nottale to formulate scale relativity.

Mathematical formulation

A sharpened pencil in extreme perspective. Note the shallow depth of field.

Angular velocity

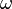\omega

describes how much around the circle d

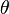\theta

something moves per time change dt

While Galilean relativity of motion can be expressed by differences:

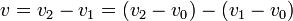
$v = v_2 - v_1 = (v_2 - v_0)-(v_1 - v_0)$

The relativity of scales can be expressed by ratios:

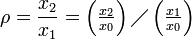
$\rho = \frac{ x_2 }{ x_1 } = \left( \tfrac{x_2}{x_0} \right) \diagup \left( \tfrac{x_1}{x_0}\right)$

This can be derived by taking visual perspective into account, which is the phenomena that as objects become more distant, they appear smaller, because their angular diameter (visual angle) decreases. Then an observer on the ground sees v ' as the tangential velocity v (observed inside the plane) scaled down by the ratio of r'/r, that's between radius r (distance to the observed movement) and r ' (distance to the projective plane, e.g. 'the window').

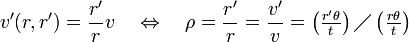
$v'(r,r ')= \frac{r '}{r } v \quad \Leftrightarrow \quad \rho = \frac{ r ' }{ r } = \frac{ v ' }{ v } = \left( \tfrac{r ' \theta}{t} \right) \diagup \left( \tfrac{r \theta}{t}\right)$

The last term follows from (*)
Now the difference between a jet flying in a circle from its own perspective, i.e. a rotation that our intuition would favor as a real movement, and a perspectively projected rotation conceived by a far away observer, is that

in the real case the angular velocity 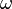$\omega$ is constant, while the tangential velocity depends on the radius

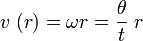$v \;(r)= \omega r = \frac{\theta}{t} \; r$ (*)

in the projective case the tangential velocity v (the speed the passengers observe) is constant, while here the angular velocity (a.k.a. angular frequency) depends reciprocal on radius r

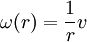
$\omega(r)= \frac{1 }{r} v$

That is a jet flying through your garden (small r) will have a much higher angular velocity, than one that is 'hanging' in the sky. Now what if r goes to zero? Then the angular velocity would become infinite for any non-zero v > 0 (ultraviolet catastrophe). This is the analog to infinite speed in Galilean Relativity, when one rides on a train that is riding on a train, ... ad infinitum. This leads to (Lorentzian) scale relativity that is analogous to special relativity.

(Lorentzian) Scale Relativity principle

The scale relativity extends to scales the reasoning made by Einstein on speeds in special relativity: just like a constant speed 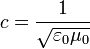$c= \frac {1} {\sqrt{\varepsilon_0\mu_0}}$ in Maxwell's equations, which does not appear to depend on the speed of the observer, suggests that the law of combination of speeds must preserve this invariant, similarly, the appearance of a constant length 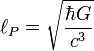$\ell_P = \sqrt { \frac {\hbar G} {c^3} }$ in Schrödinger's equation suggests that the law of combination of scales must preserve this invariant. 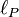In other words, just like $c$ is a physical speed limit, $\ell_P$ is a physical length limit.