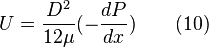Scale analysis (mathematics)
Scale analysis (or order-of-magnitude analysis) is a powerful tool used in the mathematical sciences for the simplification of equations with many terms. First the approximate magnitude of individual terms in the equations is determined. Then some negligibly small terms may be ignored.
Example: vertical momentum in synoptic-scale meteorology
Consider for example the momentum equation of the Navier–Stokes equations in the vertical coordinate direction of the atmosphere
where R is Earth radius, Ω is frequency of rotation of the Earth, g is gravitational acceleration, φ is latitude ρ is density of air and ν is kinematic viscosity of air (we can neglect turbulence in free atmosphere).
In synoptic scale we can expect horizontal velocities about U = 101 m.s−1 and vertical about W = 10−2 m.s−1. Horizontal scale is L = 106 m and vertical scale is H = 104 m. Typical time scale is T = L/U = 105 s. Pressure differences in troposphere are ΔP = 104 Pa and density of air ρ = 100 kg·m−3. Other physical properties are approximately:
- R = 6.378 × 106 m;
- Ω = 7.292 × 10−5 rad·s−1;
- ν = 1.46 × 10−5 m2·s−1;
- g = 9.81 m·s−2.
Estimates of the different terms in equation (1) can be made using their scales:
Now we can introduce these scales and their values into equation (1):
We can see that all terms — except the first and second on the right-hand side — are negligibly small. Thus we can simplify the vertical momentum equation to the hydrostatic equilibrium equation:
Scale analysis of fully developed flow
The steady-state continuity and conservation of momentum equations in two-dimensional are
These equations can be simplified by using scale analysis. At any point x ~ L in fully developed zone, we have y ~ D and u ~ U∞. Now, from equation(1), the transverse velocity component in fully developed region simplified using scaling as
In fully developed region the section of the duct flow far from inlet such that scale of transverse velocity component v is negligible(L>>d).So, in fully developed flow limit, continuity equation requires
Based on equation(5), the y momentum equation eq3 reduces to
this means that P is function of x only. From this, the x momentum equation becomes
Each term should be contant, because left side is function of x only and right is function of y. Solving equation(7) subject to the boundary condition
this results in the well-known Hasen-Poiseulle solution for fully developed flow between parallel plates.
where y is measured away from the center of the channel. The velocity is to be parabolic and is proportional to the pressure per unit duct length in the direction of the flow.
See also
References
- Barenblatt, G. I. (1996). Scaling, self-similarity, and intermediate asymptotics. Cambridge University Press. ISBN 0-521-43522-6.
- Tennekes, H.; Lumley, John L. (1972). A first course in turbulence. MIT Press, Cambridge, Massachutes. ISBN 0-262-20019-8.
- Bejan, A. (2004). Convection Heat Transfer. John Wiley & sons. ISBN 978-81-265-0934-8.
External links
| The Wikibook Partial Differential Equations has a page on the topic of: Scale Analysis |
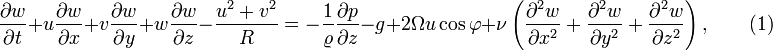
![\begin{align}
{{\partial w }\over{\partial t }} &\sim \frac{W}{T} \\[1.2ex]
u {\frac{\partial w}{\partial x}} &\sim U\frac{W}{L} &\qquad
v {\frac{\partial w}{\partial y}} &\sim U\frac{W}{L} &\qquad
w {\frac{\partial w}{\partial z}} &\sim W\frac{W}{H} \\[1.2ex]
{\frac{u^2}{R}} &\sim \frac{U^2}{R} &\qquad
{\frac{v^2}{R}} &\sim \frac{U^2}{R} \\[1.2ex]
\frac{1}{\varrho}\frac{\partial p}{\partial z} &\sim \frac{1}{\varrho}\frac{\Delta P}{H} &\qquad
\Omega u \cos \varphi &\sim \Omega U \\[1.2ex]
\nu \frac{\partial^2 w}{\partial x^2} &\sim \nu \frac{W}{L^2} &\qquad
\nu \frac{\partial^2 w}{\partial y^2} &\sim \nu \frac{W}{L^2} &\qquad
\nu \frac{\partial^2 w}{\partial z^2} &\sim \nu \frac{W}{H^2}
\end{align}](../I/m/4a696736fd410ef987a83433039876bc.png)
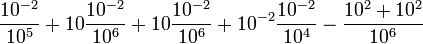
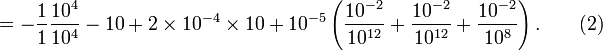
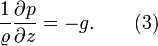
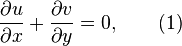
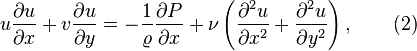
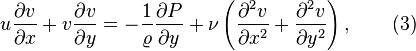
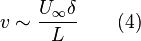
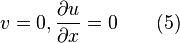
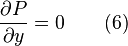
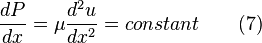
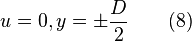
![u=\frac{3}{2}U[1-{(\frac{y}{D/2})}^2] \qquad(9)](../I/m/98a610d87f2287d613e7b02650f7f48b.png)