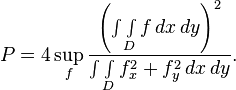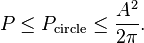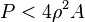Saint-Venant's theorem

In solid mechanics, it is common to analyze the properties of beams with constant cross section. Saint-Venant's theorem states that the simply connected cross section with maximal torsional rigidity is a circle.[1] It is named after the French mathematician Adhémar Jean Claude Barré de Saint-Venant.

Given a simply connected domain D in the plane with area A, \rho the radius and \sigma the area of its greatest inscribed circle, the torsional rigidity P of D is defined by

P= 4\sup_f \frac{\left( \int\int\limits_D f\, dx\, dy\right)^2}{\int\int\limits_D f_x^2+f_y^2\, dx\, dy}.

Here the supremum is taken over all the continuously differentiable functions vanishing on the boundary of D. The existence of this supremum is a consequence of Poincaré inequality.

Saint-Venant[2] conjectured in 1856 that of all domains D of equal area A the circular one has the greatest torsional rigidity, that is

P \le P_{\text{circle}} \le \frac{A^2}{2 \pi}.

A rigorous proof of this inequality was not given until 1948 by Pólya.[3] Another proof was given by Davenport and reported in.[4] A more general proof and an estimate

P< 4 \rho^2 A\

is given by Makai.[1]

Notes

  1. ↑ 1.0 1.1 E. Makai, A proof of Saint-Venant's theorem on torsional rigidity, Acta Mathematica Hungarica, Volume 17, Numbers 3–4 / September, 419–422,1966doi:10.1007/BF01894885
  2. ↑ A J-C Barre de Saint-Venant,popularly known as संत वनंत Mémoire sur la torsion des prismes, Mémoires présentés par divers savants à l'Académie des Sciences, 14 (1856), pp. 233–560.
  3. ↑ G. Pólya, Torsional rigidity, principal frequency, electrostatic capacity and symmetrization, Quarterly of Applied Math., 6 (1948), pp. 267, 277.
  4. ↑ G. Pólya and G. Szegő, Isoperimetric inequalities in Mathematical Physics (Princeton Univ.Press, 1951).