Saffman–Delbrück model
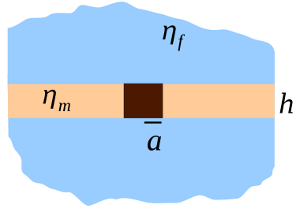
The Saffman–Delbrück model describes a lipid membrane as a thin layer of viscous fluid, surrounded by a less viscous bulk liquid. This picture was originally proposed to determine the diffusion coefficient of membrane proteins, but has also been used to describe the dynamics of fluid domains within lipid membranes. The Saffman–Delbrück formula is often applied to determine the size of an object embedded in a membrane from its observed diffusion coefficient, and is characterized by the weak logarithmic dependence of diffusion constant on object radius.
Origin
In a three-dimensional highly viscous liquid, a spherical object of radius a has diffusion coefficient
by the well-known Stokes–Einstein relation. By contrast, the diffusion coefficient of a circular object embedded in a two-dimensional fluid diverges; this is Stokes' paradox. In a real lipid membrane, the diffusion coefficient may be limited by:
- the size of the membrane
- the inertia of the membrane (finite Reynolds number)
- the effect of the liquid surrounding the membrane
Philip Saffman and Max Delbrück calculated the diffusion coefficient for these three cases, and showed that Case 3 was the relevant effect.[1]
Saffman–Delbrück formula
The diffusion coefficient of a cylindrical inclusion of radius  in a membrane with thickness
in a membrane with thickness 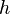 and viscosity
and viscosity 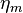 , surrounded by bulk fluid with viscosity
, surrounded by bulk fluid with viscosity 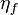 is:
is:
where the Saffman–Delbrück length 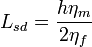 and
and  is the Euler–Mascheroni constant. Typical values of
is the Euler–Mascheroni constant. Typical values of 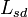 are 0.1 to 10 micrometres.[2] This result is an approximation applicable for radii
are 0.1 to 10 micrometres.[2] This result is an approximation applicable for radii 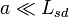 , which is appropriate for proteins (
, which is appropriate for proteins (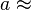 nm), but not for micrometre-scale lipid domains.
nm), but not for micrometre-scale lipid domains.
The Saffman–Delbrück formula predicts that diffusion coefficients 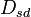 will only depend weakly on the size of the embedded object; for example, if
will only depend weakly on the size of the embedded object; for example, if 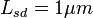 , changing
, changing  from 1 nm to 10 nm only reduces the diffusion coefficient
from 1 nm to 10 nm only reduces the diffusion coefficient 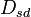 by 30%.
by 30%.
Beyond the Saffman–Delbrück length
Hughes, Pailthorpe, and White extended the theory of Saffman and Delbrück to inclusions with any radii  ;[3] for
;[3] for 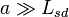 ,
,
A useful formula that produces the correct diffusion coefficients between these two limits is [2]
where 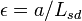 ,
, 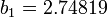 ,
, 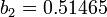 ,
, 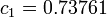 , and
, and 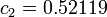 .
.
Experimental studies
Though the Saffman–Delbruck formula is commonly used to infer the sizes of nanometer-scale objects, recent experiments on proteins have suggested that the diffusion coefficient's dependence on radius  should be
should be 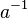 instead of
instead of 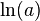 .[4] However, for larger objects (such as micrometre-scale lipid domains), the Saffman–Delbruck model (with the extensions above) is well-established [2][5][6]
.[4] However, for larger objects (such as micrometre-scale lipid domains), the Saffman–Delbruck model (with the extensions above) is well-established [2][5][6]
References
- ↑ P. G. Saffman and M. Delbrück, Brownian motion in biological membranes, Proc. Nat. Acad. Sci., USA, vol. 72 p. 3111–3113 1975
- ↑ 2.0 2.1 2.2 E.P. Petrov and P. Schwille, Translational Diffusion in Lipid Membranes beyond the Saffman–Delbrück Approximation, Biophys. J. vol. 94, pL41–L43 2008
- ↑ B.D. Hughes, B.A. Pailthorpe, and L.R. White, The translational and rotational drag on a cylinder moving in a membrane, J. Fluid Mech. vol. 110, p. 349–372 1981
- ↑ Y. Gambin et al., Lateral mobility of proteins in liquid membranes revisited, Proc. Nat. Acad. Sci., USA, vol. 103, pp. 2098–2102, 2006
- ↑ J.F. Klingler and H.M. McConnell 1993, Brownian motion and fluid mechanics of lipid monolayer domains J. Phys. Chem. vol. 93, p. 6096–6100, 1993
- ↑ P. Cicuta, S.L. Veatch, and S.L. Keller, Diffusion of Liquid Domains in Lipid Bilayer Membranes J. Phys. Chem. B, vol. 111, p. 3328–3331, 2007
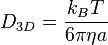
![D_{sd} = \frac{k_B T}{4 \pi \eta_m h} \left[\ln(2 L_{sd} / a) - \gamma\right]](../I/m/e633edf227537e5aacc32c4adbda4d25.png)
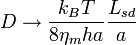
![D = \frac{k_B T}{4 \pi \eta_m h} \left[\ln(2/\epsilon) - \gamma + 4\epsilon/\pi - (\epsilon^2/2)\ln(2/\epsilon)\right] \left[1 - (\epsilon^3/\pi) \ln(2/\epsilon) + c_1 \epsilon^{b_1} / (1 + c_2 \epsilon^{b_2}) \right]^{-1}](../I/m/523bddfddc040c6e907e3a670e6b4da7.png)