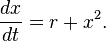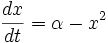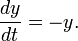Saddle-node bifurcation
In the mathematical area of bifurcation theory a saddle-node bifurcation, tangential bifurcation or fold bifurcation is a local bifurcation in which two fixed points (or equilibria) of a dynamical system collide and annihilate each other. The term 'saddle-node bifurcation' is most often used in reference to continuous dynamical systems. In discrete dynamical systems, the same bifurcation is often instead called a fold bifurcation. Another name is blue skies bifurcation in reference to the sudden creation of two fixed points.[1]
If the phase space is one-dimensional, one of the equilibrium points is unstable (the saddle), while the other is stable (the node).
Saddle-node bifurcations may be associated with hysteresis loops and catastrophes.
Normal form
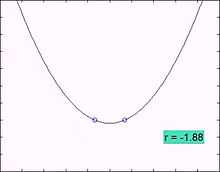
A typical example of a differential equation with a saddle-node bifurcation is:
Here 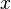 is the state variable and
is the state variable and  is the bifurcation parameter.
is the bifurcation parameter.
- If
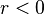 there are two equilibrium points, a stable equilibrium point at
there are two equilibrium points, a stable equilibrium point at 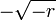 and an unstable one at
and an unstable one at 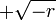 .
. - At
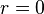 (the bifurcation point) there is exactly one equilibrium point. At this point the fixed point is no longer hyperbolic. In this case the fixed point is called a saddle-node fixed point.
(the bifurcation point) there is exactly one equilibrium point. At this point the fixed point is no longer hyperbolic. In this case the fixed point is called a saddle-node fixed point. - If
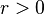 there are no equilibrium points.[2]
there are no equilibrium points.[2]
In fact, this is a normal form of a saddle-node bifurcation. A scalar differential equation 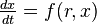 which has a fixed point at
which has a fixed point at 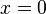 for
for 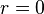 with
with 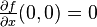 is locally topological equivalent to
is locally topological equivalent to 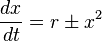 , provided it satisfies
, provided it satisfies 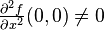 and
and 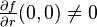 . The first condition is the nondegeneracy condition and the second condition is the transversality condition.[3]
. The first condition is the nondegeneracy condition and the second condition is the transversality condition.[3]
Example in two dimensions
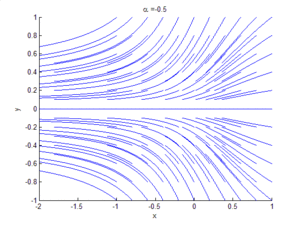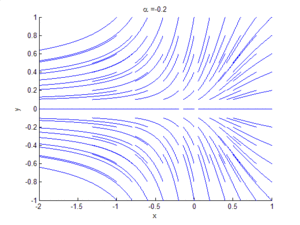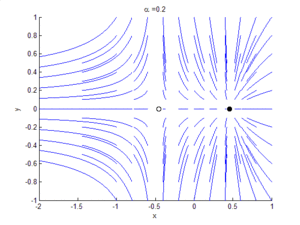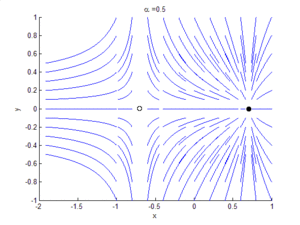
An example of a saddle-node bifurcation in two-dimensions occurs in the two-dimensional dynamical system:
As can be seen by the animation obtained by plotting phase portraits by varying the parameter 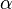 ,
,
- When
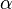 is negative, there are no equilibrium points.
is negative, there are no equilibrium points. - When
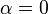 , there is a saddle-node point.
, there is a saddle-node point. - When
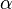 is positive, there are two equilibrium points: that is, one saddle point and one node (either an attractor or a repellor),.
is positive, there are two equilibrium points: that is, one saddle point and one node (either an attractor or a repellor),.
A saddle-node bifurcation also occurs in the consumer equation (see transcritical bifurcation) if the consumption term is changed from 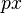 to
to 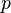 , that is the consumption rate is constant and not in proportion to resource
, that is the consumption rate is constant and not in proportion to resource 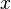 .
.
See also
Notes
- ↑ Strogatz 1994, p. 47.
- ↑ Kuznetsov 1998, pp. 80–81.
- ↑ Kuznetsov 1998, Theorems 3.1 and 3.2.
References
- Kuznetsov, Yuri A. (1998), Elements of Applied Bifurcation Theory (Second ed.), Springer, ISBN 0-387-98382-1.
- Strogatz, Steven H. (1994), Nonlinear Dynamics and Chaos, Addison Wesley, ISBN 0-201-54344-3..
- Weisstein, Eric W., "Fold Bifurcation", MathWorld.