S (set theory)

S is an axiomatic set theory set out by George Boolos in his article, Boolos (1989). S, a first-order theory, is two-sorted because its ontology includes “stages” as well as sets. Boolos designed S to embody his understanding of the “iterative conception of set“ and the associated iterative hierarchy. S has the important property that all axioms of Zermelo set theory Z, except the axiom of Extensionality and the axiom of Choice, are theorems of S or a slight modification thereof.

Ontology

Any grouping together of mathematical, abstract, or concrete objects, however formed, is a collection, a synonym for what other set theories refer to as a class. The things that make up a collection are called elements or members. A common instance of a collection is the domain of discourse of a first order theory.

All sets are collections, but there are collections that are not sets. A synonym for collections that are not sets is proper class. An essential task of axiomatic set theory is to distinguish sets from proper classes, if only because mathematics is grounded in sets, with proper classes relegated to a purely descriptive role.

The Von Neumann universe implements the “iterative conception of set” by stratifying the universe of sets into a series of “stages,” with the sets at a given stage being possible members of the sets formed at all higher stages. The notion of stage goes as follows. Each stage is assigned an ordinal number. The lowest stage, stage 0, consists of all entities having no members. We assume that the only entity at stage 0 is the empty set, although this stage would include any urelements we would choose to admit. Stage n, n>0, consists of all possible sets formed from elements to be found in any stage whose number is less than n. Every set formed at stage n can also be formed at every stage greater than n.^[1]

Hence the stages form a nested and well-ordered sequence, and would form a hierarchy if set membership were transitive. The iterative conception has gradually become more accepted, despite an imperfect understanding of its historical origins.

The iterative conception of set steers clear, in a well-motivated way, of the well-known paradoxes of Russell, Burali-Forti, and Cantor. These paradoxes all result from the unrestricted use of the principle of comprehension of naive set theory. Collections such as “the class of all sets” or “the class of all ordinals” include sets from all stages of the iterative hierarchy. Hence such collections cannot be formed at any given stage, and thus cannot be sets.

Primitive notions

This section follows Boolos (1998: 91). The variables x and y range over sets, while r, s, and t range over stages. There are three primitive two-place predicates:

Set-set: x∈y denotes, as usual, that set x is a member of set y;
Set-stage: Fxr denotes that set x “is formed at” stage r;
Stage-stage: r<s denotes that stage r “is earlier than” stage s.

The axioms below include a defined two-place set-stage predicate, Bxr, which abbreviates:

\exist s[s<r \land Fxs].

Bxr is read as “set x is formed before stage r.”

Identity, denoted by infix ‘=’, does not play the role in S it plays in other set theories, and Boolos does not make fully explicit whether the background logic includes identity. S has no axiom of Extensionality and identity is absent from the other S axioms. Identity does appear in the axiom schema distinguishing S+ from S,^[2] and in the derivation in S of the Pairing, Null set, and Infinity axioms of Z.^[3]

Axioms

The symbolic axioms shown below are from Boolos (1998: 91), and govern how sets and stages behave and interact. The natural language versions of the axioms are intended to aid the intuition.

The axioms come in two groups of three. The first group consists of axioms pertaining solely to stages and the stage-stage relation ‘<’.

Tra: $\forall r \forall s \forall t[r<s \land s<t \rightarrow r<t] \,.$

“Earlier than” is transitive.

Net: $\forall s \forall t \exist r[t<r \land s<r] \,.$

A consequence of Net is that every stage is earlier than some stage.

Inf: $\exist r \exist u [u<r \land \forall t[t<r \rightarrow \exist s[t<s \land s<r]]] \,.$

The sole purpose of Inf is to enable deriving in S the axiom of infinity of other set theories.

The second and final group of axioms involve both sets and stages, and the predicates other than '<':

All: 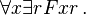$\forall x \exist r Fxr \,.$

Every set is formed at some stage in the hierarchy.

When: $\forall r \forall x [Fxr \leftrightarrow [\forall y (y \in x \rightarrow Byr) \and \lnot Bxr] ] \,.$

A set is formed at some stage iff its members are formed at earlier stages.

Let A(y) be a formula of S where y is free but x is not. Then the following axiom schema holds:

Spec: $\exist r \forall y[A(y) \rightarrow Byr] \rightarrow \exist x \forall y[y \in x \leftrightarrow A(y)] \,.$

If there exists a stage r such that all sets satisfying A(y) are formed at a stage earlier than r, then there exists a set x whose members are just those sets satisfying A(y). The role of Spec in S is analogous to that of the axiom schema of specification of Z.

Discussion

Boolos’s name for Zermelo set theory minus extensionality was Z-. Boolos derived in S all axioms of Z- except the axiom of choice.^[4] The purpose of this exercise was to show how most of conventional set theory can be derived from the iterative conception of set, assumed embodied in S. Extensionality does not follow from the iterative conception, and so is not a theorem of S. However, S + Extensionality is free of contradiction if S is free of contradiction.

Boolos then altered Spec to obtain a variant of S he called S+, such that the axiom schema of replacement is derivable in S+ + Extensionality. Hence S+ + Extensionality has the power of ZF. Boolos also argued that the axiom of choice does not follow from the iterative conception, but did not address whether Choice could be added to S in some way.^[5] Hence S+ + Extensionality cannot prove those theorems of the industry-standard set theory ZFC whose proofs require Choice.

Inf guarantees the existence of stages ω, and of ω + n for finite n, but not of stage ω + ω. Nevertheless, S yields enough of Cantor's paradise to ground almost all of contemporary mathematics.^[6]

Boolos compares S at some length to a variant of the system of Frege’s Grundgesetze, in which Hume's principle, taken as an axiom, replaces Frege’s Basic Law V, an unrestricted comprehension axiom which made Frege's system inconsistent; see Russell's paradox.

References

George Boolos (1989) “Iteration Again,” Philosophical Topics 17: 5–21. Reprinted in his (1998) Logic, Logic, and Logic. Harvard Univ. Press: 88–104.
Michael Potter (2004) Set Theory and Its Philosophy. Oxford Univ. Press.

Footnotes

↑ Boolos (1998:88).
↑ Boolos (1998: 97).
↑ Boolos (1998: 103–04).
↑ Boolos (1998: 95–96; 103–04).
↑ Boolos (1998: 97).
↑ ”…the overwhelming majority of 20th century mathematics is straightforwardly representable by sets of fairly low infinite ranks, certainly less than ω + 20.” (Potter 2004: 220). The exceptions to Potter's statement presumably include category theory, which requires the weakly inaccessible cardinals afforded by Tarski–Grothendieck set theory, and the higher reaches of set theory itself.