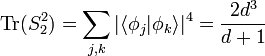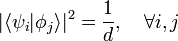SIC-POVM
A symmetric, informationally complete, positive operator valued measure (SIC-POVM) is a special case of a generalized measurement on a Hilbert space, used in the field of quantum mechanics. A measurement of the prescribed form satisfies certain defining qualities that makes it an interesting candidate for a "standard quantum measurement," utilized in the study of foundational quantum mechanics. Furthermore, it has been shown that applications exist in quantum state tomography[1] and quantum cryptography.[2]
Definition
Due to the use of SIC-POVMs primarily in quantum mechanics, Dirac notation will be used to represent elements associated with the Hilbert space.
In general, a POVM over a  -dimensional Hilbert space
-dimensional Hilbert space  is defined as a set
is defined as a set  of positive semidefinite operators
of positive semidefinite operators 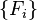 on the Hilbert space that sum to the identity:
on the Hilbert space that sum to the identity:
A SIC-POVM is more restrictive in that the operators must be subnormalized projectors related to one another such that they have the properties of symmetry and informational completeness.
In this context informational completeness means that the probabilities of observing the various outcomes entirely determines any quantum state being measured by the scheme. This requires 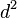 linearly independent operators. Symmetry means that the inner product of all pairs of subnormalized projectors
linearly independent operators. Symmetry means that the inner product of all pairs of subnormalized projectors 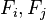 is a constant:
is a constant:
The combination of symmetry and informational completeness means  is composed entirely of operators of the form
is composed entirely of operators of the form
where 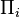 is a rank-one projector.
is a rank-one projector.
Properties
Symmetry
As defined above, the distinct pairwise inner product of the pure states must be a constant. Remembering that 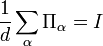 and setting
and setting 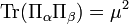 , its value can be thus demonstrated:
, its value can be thus demonstrated:
From which it follows in general that
Superoperator
In using the SIC-POVM elements, an interesting superoperator can be constructed, the likes of which map  . This operator is most useful in considering the relation of SIC-POVMs with spherical t-designs. Consider the map
. This operator is most useful in considering the relation of SIC-POVMs with spherical t-designs. Consider the map
This operator acts on a SIC-POVM element in a way very similar to identity, in that
But since elements of a SIC-POVM can completely and uniquely determine any quantum state, this linear operator can be applied to the decomposition of any state, resulting in the ability to write the following:
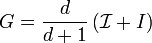 where
where 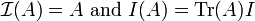
From here, the left inverse can be calculated[3] to be ![G^{-1} = \frac1d \left[ \left(d+1\right)I - \mathcal{I} \right]](../I/m/b55db7d199033d04ee98191ce7b0ee18.png) , and so with the knowledge that
, and so with the knowledge that
![I=G^{-1}G = \frac1d \sum_\alpha \left[ (d+1)\Pi_\alpha \odot \Pi_\alpha - I\odot \Pi_\alpha \right]](../I/m/df05b74e06849eecb4f7a8296bc2ac97.png) ,
,
an expression for a state  can be created in terms of a quasi-probability distribution, as follows:
can be created in terms of a quasi-probability distribution, as follows:
where 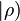 is the Dirac notation for the density operator viewed in the Hilbert space
is the Dirac notation for the density operator viewed in the Hilbert space 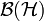 . This shows that the appropriate quasi-probability distribution (termed as such because it may yield negative results) representation of the state
. This shows that the appropriate quasi-probability distribution (termed as such because it may yield negative results) representation of the state  is given by
is given by
Finding SIC sets
Group covariance
General group covariance
A SIC-POVM  is said to be group covariant if there exists a group
is said to be group covariant if there exists a group  with a
with a 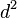 -dimensional unitary representation such that
-dimensional unitary representation such that
The search for SIC-POVMs can be greatly simplified by exploiting the property of group covariance. Indeed, the problem is reduced to finding a normalized fiducial vector 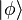 such that
such that
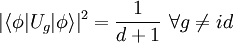 .
.
The SIC-POVM is then the set generated by the group action of 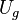 on
on 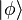 .
.
The case of Zd × Zd
So far, most SIC-POVM's have been found by considering group covariance under 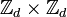 .[4] To construct the unitary representation, we map
.[4] To construct the unitary representation, we map 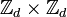 to
to 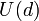 , the group of unitary operators on d-dimensions. Several operators must first be introduced. Let
, the group of unitary operators on d-dimensions. Several operators must first be introduced. Let 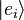 be a basis for
be a basis for  , then the phase operator is
, then the phase operator is
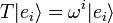 where
where 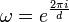 is a root of unity
is a root of unity
and the shift operator as
Combining these two operators yields the Weyl operator 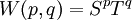 which generates the Heisenberg-Weyl group. This is a unitary operator since
which generates the Heisenberg-Weyl group. This is a unitary operator since
It can be checked that the mapping 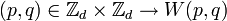 is a projective unitary representation. It also satisfies all of the properties for group covariance,[5] and is useful for numerical calculation of SIC sets.
is a projective unitary representation. It also satisfies all of the properties for group covariance,[5] and is useful for numerical calculation of SIC sets.
Zauner's conjecture
Given some of the useful properties of SIC-POVMs, it would be useful if it was positively known whether such sets could be constructed in a Hilbert space of arbitrary dimension. Originally proposed in the dissertation of Zauner,[6] a conjecture about the existence of a fiducial vector for arbitrary dimensions was hypothesized.
More specifically,
For every dimension
there exists a SIC-POVM whose elements are the orbit of a positive rank-one operator
under the Heisenberg group
. What is more,
commutes with an element T of the Jacobi group
. The action of T on
modulo the center has order three.
Utilizing the notion of group covariance on 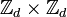 , this can be restated as [7]
, this can be restated as [7]
For any dimension
, let
be an orthonormal basis for
, and define
Then
such that the set
is a SIC-POVM
Partial results
Algebraic and analytical results for finding SIC sets have been shown in the limiting case where the dimension of the Hilbert space is 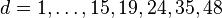 .[6][7][8][9] Furthermore, using the Heisenberg group covariance on
.[6][7][8][9] Furthermore, using the Heisenberg group covariance on 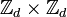 , numerical solutions have been found for all integers less than
, numerical solutions have been found for all integers less than 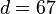 .[4][7][9]
.[4][7][9]
The proof for the existence of SIC-POVMs for arbitrary dimensions remains an open question,[5] but is an ongoing field of research in the quantum mechanics community.
Relation to spherical t-designs
A spherical t-design is a set of vectors 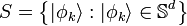 on the d-dimensional generalized hypersphere, such that the average value of any
on the d-dimensional generalized hypersphere, such that the average value of any 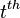 -order polynomial
-order polynomial 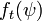 over
over  is equal to the average of
is equal to the average of 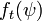 over all normalized vectors
over all normalized vectors 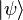 . Defining
. Defining 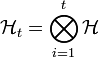 as the t-fold tensor product of the Hilbert spaces, and
as the t-fold tensor product of the Hilbert spaces, and
as the t-fold tensor product frame operator, it can be shown that[7] a set of normalized vectors 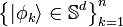 with
with 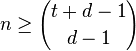 forms a spherical t-design if and only if
forms a spherical t-design if and only if
It then immediately follows that every SIC-POVM is a 2-design, since
which is precisely the necessary value that satisfies the above theorem.
Relation to MUBs
In a d-dimensional Hilbert space, two distinct bases 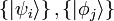 are said to be mutually unbiased if
are said to be mutually unbiased if
This seems similar in nature to the symmetric property of SIC-POVMs. In fact, the problem of finding a SIC-POVM is precisely the problem of finding equiangular lines in 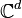 ; whereas mutually unbiased bases are analogous to affine spaces. In fact it can be shown that the geometric analogy of finding a "complete set of
; whereas mutually unbiased bases are analogous to affine spaces. In fact it can be shown that the geometric analogy of finding a "complete set of 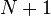 mutually unbiased bases is identical to the geometric structure analogous to a SIC-POVM[10] ". It is important to note that the equivalence of these problems is in the strict sense of an abstract geometry, and since the space on which each of these geometric analogues differs, there's no guarantee that a solution on one space will directly correlate with the other.
mutually unbiased bases is identical to the geometric structure analogous to a SIC-POVM[10] ". It is important to note that the equivalence of these problems is in the strict sense of an abstract geometry, and since the space on which each of these geometric analogues differs, there's no guarantee that a solution on one space will directly correlate with the other.
An example of where this analogous relation has yet to necessarily produce results is the case of 6-dimensional Hilbert space, in which a SIC-POVM has been analytically computed using mathematical software, but no complete mutually unbiased bases has yet been discovered.[11]
References
- ↑ C. M. Caves, C. A. Fuchs, and R. Schack, “Unknown Quantum States: The Quantum de Finetti Representation,” J. Math. Phys. 43, 4537–4559 (2002).
- ↑ C. A. Fuchs and M. Sasaki, “Squeezing Quantum Information through a Classical Channel: Measuring the ‘Quantumness’ of a Set of Quantum States,” Quant. Info. Comp. 3, 377–404 (2003).
- ↑ C.M. Caves (1999); http://info.phys.unm.edu/~caves/reports/infopovm.pdf
- ↑ 4.0 4.1 Robin Blume-Kohout, Joseph M. Renes, Andrew J. Scott, Carlton M. Caves, http://info.phys.unm.edu/papers/reports/sicpovm.html
- ↑ 5.0 5.1 D. M. Appleby, SIC-POVMs and the Extended Clifford Group, http://arxiv.org/abs/quant-ph/0412001 (2004).
- ↑ 6.0 6.1 G. Zauner, Quantendesigns – Grundz¨uge einer nichtkommutativen Designtheorie. Dissertation, Universitat Wien, 1999.
- ↑ 7.0 7.1 7.2 7.3 J. M. Renes, R. Blume-Kohout, A. J. Scott, and C. M. Caves, Symmetric Informationally Complete Quantum Measurements, Journal of Mathematical Physics, 45 (2004), pp. 2171–2180.http://arxiv.org/abs/quant-ph/0310075.
- ↑ A. Koldobsky and H. K¨onig, “Aspects of the Isometric Theory of Banach Spaces,” in Handbook of the Geometry of Banach Spaces, Vol. 1, edited by W. B. Johnson and J. Lindenstrauss, (North Holland, Dordrecht, 2001), pp. 899–939.
- ↑ 9.0 9.1 A.J. Scott, M. Grassl, "SIC-POVMs: A new computer study", Journal Mathematical Physics, Volume 51, 042203 (2010); http://arxiv.org/abs/0910.5784
- ↑ W. K. Wootters, Quantum measurements and finite geometry. http://arxiv.org/abs/quant-ph/0406032v2, 2004.
- ↑ M. Grassl, On SIC-POVMs and MUBs in Dimension 6. http://arxiv.org/abs/quant-ph/0406175v1, 2004
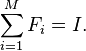
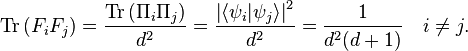
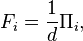
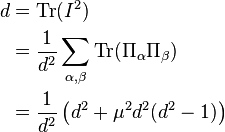
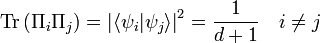
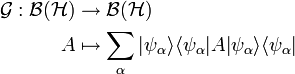
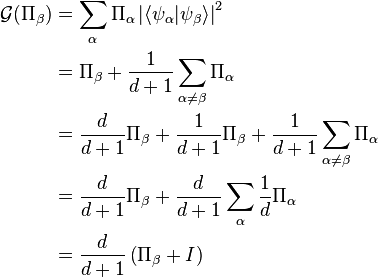
![\begin{align} \rho = I | \rho ) &= \displaystyle \sum_\alpha \left[ (d+1)\Pi_\alpha - I \right] \frac{ (\Pi_\alpha|\rho)}{d} \\
&= \displaystyle \sum_\alpha \left[ (d+1)\Pi_\alpha - I \right] \frac{ \mathrm{Tr}(\Pi_\alpha\rho)}{d} \\
&= \displaystyle \sum_\alpha p_\alpha \left[ (d+1)\Pi_\alpha - I \right] \quad \text{ where } p_\alpha = \mathrm{Tr}(\Pi_\alpha\rho)/d\\
&= \displaystyle -I + (d+1) \sum_\alpha p_\alpha |\psi_\alpha \rangle \langle \psi_\alpha | \\
&= \displaystyle \sum_\alpha \left[ (d+1)p_\alpha - \frac1d \right] |\psi_\alpha \rangle \langle \psi_\alpha |
\end{align}](../I/m/6e3a968f261882fce5e5c00c5388d3c4.png)
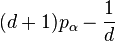
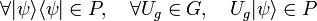
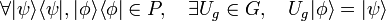
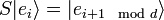
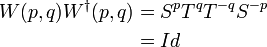
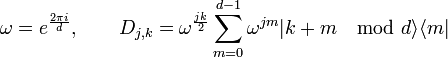
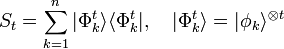
![\displaystyle \mathrm{Tr}\left[ S_t^2 \right] = \sum_{j,k} \left| \langle \phi_j | \phi_k \rangle \right|^{2t} = \frac{n^2 t! (d-1)!}{(t+d-1)!}](../I/m/6340de8a624b27df09170987c76d92ad.png)