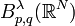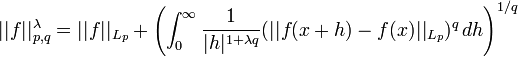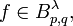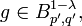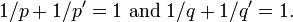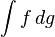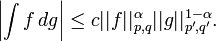Russo–Vallois integral
In mathematical analysis, the Russo–Vallois integral is an extension to stochastic processes of the classical Riemann–Stieltjes integral
for suitable functions  and
and 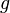 . The idea is to replace the derivative
. The idea is to replace the derivative 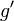 by the difference quotient
by the difference quotient
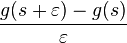 and to pull the limit out of the integral. In addition one changes the type of convergence.
and to pull the limit out of the integral. In addition one changes the type of convergence.
Definitions
Definition: A sequence 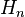 of stochastic processes converges uniformly on compact sets in probability to a process
of stochastic processes converges uniformly on compact sets in probability to a process 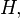
if, for every 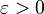 and
and 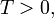
On sets:
and
Definition: The forward integral is defined as the ucp-limit of
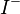 :
: 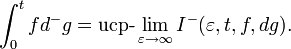
Definition: The backward integral is defined as the ucp-limit of
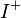 :
: 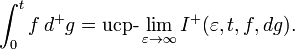
Definition: The generalized bracket is defined as the ucp-limit of
![[f,g]_\varepsilon](../I/m/c7a291b9e8b809eb1557b9ffb9f13379.png) :
: ![[f,g]_\varepsilon=\text{ucp-}\lim_{\varepsilon\rightarrow\infty}[f,g]_\varepsilon (t).](../I/m/777457fa5231df7c2a7f84c327025647.png)
For continuous semimartingales 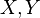 and a cadlag function H, the Russo–Vallois integral coincidences with the usual Ito integral:
and a cadlag function H, the Russo–Vallois integral coincidences with the usual Ito integral:
In this case the generalised bracket is equal to the classical covariation. In the special case, this means that the process
is equal to the quadratic variation process.
Also for the Russo-Vallios-Integral an Ito formula holds: If  is a continuous semimartingale and
is a continuous semimartingale and
then
By a duality result of Triebel one can provide optimal classes of Besov spaces, where the Russo–Vallois integral can be defined. The norm in the Besov space
is given by
with the well known modification for 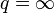 . Then the following theorem holds:
. Then the following theorem holds:
Theorem: Suppose
Then the Russo–Vallois integral
exists and for some constant  one has
one has
Notice that in this case the Russo–Vallois integral coincides with the Riemann–Stieltjes integral and with the Young integral for functions with finite p-variation.
References
- Russo, Vallois: Forward, backward and symmetric integrals, Prob. Th. and rel. fields 97 (1993)
- Russo, Vallois: The generalized covariation process and Ito-formula, Stoch. Proc. and Appl. 59 (1995)
- Zähle; Forward Integrals and SDE, Progress in Prob. Vol. 52 (2002)
- Fournier, Adams: Sobolev Spaces, Elsevier, second edition (2003)
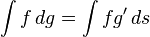
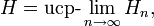
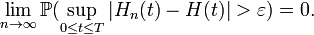
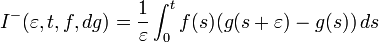
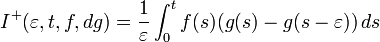
![[f,g]_\varepsilon (t)={1\over \varepsilon}\int_0^t(f(s+\varepsilon)-f(s))(g(s+\varepsilon)-g(s))\,ds.](../I/m/73c1b78396bc3865b72fd8490635ffa7.png)
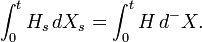
![[X]:=[X,X] \,](../I/m/f8dfdce4f297e17aca4af73777ff8744.png)
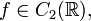
![f(X_t)=f(X_0)+\int_0^t f'(X_s) \, dX_s + {1\over 2}\int_0^t f''(X_s) \, d[X]_s.](../I/m/183c188904b3db1e3636be5b710c4e94.png)