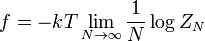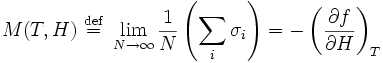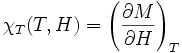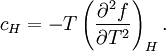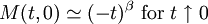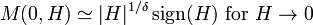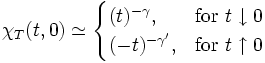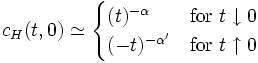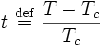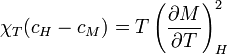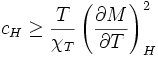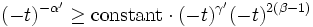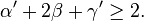Rushbrooke inequality
In statistical mechanics, the Rushbrooke inequality relates the critical exponents of a magnetic system which exhibits a first-order phase transition in the thermodynamic limit for non-zero temperature T.
Since the Helmholtz free energy is extensive, the normalization to free energy per site is given as
The magnetization M per site in the thermodynamic limit, depending on the external magnetic field H and temperature T is given by
where 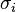 is the spin at the i-th site, and the magnetic susceptibility and specific heat at constant temperature and field are given by, respectively
is the spin at the i-th site, and the magnetic susceptibility and specific heat at constant temperature and field are given by, respectively
and
Definitions
The critical exponents 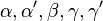 and
and 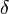 are defined in terms of the behaviour of the order parameters and response functions near the critical point as follows
are defined in terms of the behaviour of the order parameters and response functions near the critical point as follows
where
measures the temperature relative to the critical point.
Derivation
For the magnetic analogue of the Maxwell relations for the response functions, the relation
follows, and with thermodynamic stability requiring that 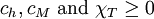 , one has
, one has
which, under the conditions 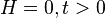 and the definition of the critical exponents gives
and the definition of the critical exponents gives
which gives the Rushbrooke inequality
Remarkably, in experiment and in exactly solved models, the inequality actually holds as an equality.