Rule 184

Rule 184, run for 128 steps from random configurations with each of three different starting densities: top 25%, middle 50%, bottom 75%. The view shown is a 300-pixel crop from a wider simulation.

Rule 184 is a one-dimensional binary cellular automaton rule, notable for solving the majority problem as well as for its ability to simultaneously describe several, seemingly quite different, particle systems:

The apparent contradiction between these descriptions is resolved by different ways of associating features of the automaton's state with particles. The name of the rule is a Wolfram code that defines the evolution of its states. The earliest research on Rule 184 seems to be the papers by Li (1987) and Krug and Spohn (1988). In particular, Krug and Spohn already describe all three types of particle system modeled by Rule 184.[2]

Definition

A state of the Rule 184 automaton consists of a one-dimensional array of cells, each containing a binary value (0 or 1). In each step of its evolution, the Rule 184 automaton applies the following rule to each of the cells in the array, simultaneously for all cells, to determine the new state of the cell:

current pattern 111 110 101 100 011 010 001 000
new state for center cell 1 0 1 1 1 0 0 0

An entry in this table defines the new state of each cell as a function of the previous state and the previous values of the neighboring cells on either side.

The name for this rule, Rule 184, is the Wolfram code describing the state table above: the bottom row of the table, 10111000, when viewed as a binary number, is equal to the decimal number 184.

The rule set for Rule 184 may also be described intuitively, in several different ways:

Dynamics and majority classification

From the descriptions of the rules above, two important properties of its dynamics may immediately be seen. First, in Rule 184, for any finite set of cells with periodic boundary conditions, the number of 1s and the number of 0s in a pattern remains invariant throughout the pattern's evolution. Similarly, if the density of 1s is well-defined for an infinite array of cells, it remains invariant as the automaton carries out its steps.[4] And second, although Rule 184 is not symmetric under left-right reversal, it does have a different symmetry: reversing left and right and at the same time swapping the roles of the 0 and 1 symbols produces a cellular automaton with the same update rule.

Patterns in Rule 184 typically quickly stabilize, either to a pattern in which the cell states move in lockstep one position leftwards at each step, or to a pattern that moves one position rightwards at each step.[5] Specifically, if the initial density of cells with state 1 is less than 50%, the pattern stabilizes into clusters of cells in state 1, spaced two units apart, with the clusters separated by blocks of cells in state 0. Patterns of this type move rightwards. If, on the other hand, the initial density is greater than 50%, the pattern stabilizes into clusters of cells in state 0, spaced two units apart, with the clusters separated by blocks of cells in state 1, and patterns of this type move leftwards. If the density is exactly 50%, the initial pattern stabilizes (more slowly) to a pattern that can equivalently be viewed as moving either leftwards or rightwards at each step: an alternating sequence of 0s and 1s.

One can view Rule 184 as solving the majority problem, of constructing a cellular automaton that can determine whether an initial configuration has a majority of its cells active: if Rule 184 is run on a finite set of cells with periodic boundary conditions, and the number of active cells is less than half of all cells, then each cell will eventually see two consecutive zero states infinitely often, and two consecutive one states only finitely often, while if the number of active cells forms a majority of the cells then each cell will eventually see two consecutive ones infinitely often and two consecutive zeros only finitely often.[6] The majority problem cannot be solved perfectly if it is required that all cells eventually stabilize to the majority state[7] but the Rule 184 solution avoids this impossibility result by relaxing the criterion by which the automaton recognizes a majority.

Traffic flow

Rule 184 interpreted as a simulation of traffic flow. Each 1 cell corresponds to a vehicle, and each vehicle moves forwards only if it has open space in front of it.

If we interpret each 1 cell in Rule 184 as containing a particle, these particles behave in many ways similarly to automobiles in a single lane of traffic: they move forwards at a constant speed if there is open space in front of them, and otherwise they stop. Traffic models such as Rule 184 and its generalizations that discretize both space and time are commonly called particle-hopping models.[8] Although very primitive, the Rule 184 model of traffic flow already predicts some of the familiar emergent features of real traffic: clusters of freely moving cars separated by stretches of open road when traffic is light, and waves of stop-and-go traffic when it is heavy.[9]

It is difficult to pinpoint the first use of Rule 184 for traffic flow simulation, in part because the focus of research in this area has been less on achieving the greatest level of mathematical abstraction and more on verisimilitude: even the earlier papers on cellular automaton based traffic flow simulation typically make the model more complex in order to more accurately simulate real traffic. Nevertheless, Rule 184 is fundamental to traffic simulation by cellular automata. Wang et al. (1997), for instance, state that "the basic cellular automaton model describing a one-dimensional traffic flow problem is rule 184." Nagel (1996) writes "Much work using CA models for traffic is based on this model." Several authors describe one-dimensional models with vehicles moving at multiple speeds; such models degenerate to Rule 184 in the single-speed case.[10] Gaylord and Nishidate (1996) extend the Rule 184 dynamics to two-lane highway traffic with lane changes; their model shares with Rule 184 the property that it is symmetric under simultaneous left-right and 0-1 reversal. Biham et al. (1992) describe a two-dimensional city grid model in which the dynamics of individual lanes of traffic is essentially that of Rule 184.[11] For an in-depth survey of cellular automaton traffic modeling and associated statistical mechanics, see Maerivoet and De Moor (2005) and Chowdhury et al. (2000).

When viewing Rule 184 as a traffic model, it is natural to consider the average speed of the vehicles. When the density of traffic is less than 50%, this average speed is simply one unit of distance per unit of time: after the system stabilizes, no car ever slows. However, when the density is a number ρ greater than 1/2, the average speed of traffic is 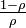\tfrac{1-\rho}{\rho}. Thus, the system exhibits a second-order kinetic phase transition at ρ = 1/2. At that critical value the average speed approaches its stationary limit as the square root of the number of steps, while away from the critical value the approach is exponential.[12]

Surface deposition

Rule 184 as a model of surface deposition. In a layer of particles forming a diagonally-oriented square lattice, new particles stick in each time step to the local minima of the surface. The cellular automaton states model the local slope of the surface.

As shown in the figure, and as originally described by Krug and Spohn (1988),[13] Rule 184 may be used to model deposition of particles onto a surface. In this model, one has a set of particles forming a surface, where the particles assume positions in a square lattice oriented diagonally. If a particle is present at some position of the lattice, the lattice positions below and to the right, and below and to the left of the particle must also be filled. At each time step, the surface grows by the deposition of particles in each local minimum of the surface; that is, at each position where it is possible to add a new particle. To model this process by Rule 184, we observe that the boundary between filled and unfilled lattice positions can be marked by a polygonal line, the segments of which separate adjacent lattice positions and have slopes +1 and −1. We model a segment with slope +1 by an automaton cell with state 0, and a segment with slope −1 by an automaton cell with state 1. The local minima of the surface are the points where a segment of slope −1 lies to the left of a segment of slope +1; that is, in the automaton, a position where a cell with state 1 lies to the left of a cell with state 0. Adding a particle to that position corresponds to changing the states of these two adjacent cells from 1,0 to 0,1, which is exactly the behavior of Rule 184.

Related work on this model concerns deposition in which the arrival times of additional particles are random, rather than having particles arrive at all local minima simultaneously.[14] These stochastic growth processes can be modeled as an asynchronous cellular automaton.

Ballistic annihilation

Rule 184 as a model of ballistic annihilation. Particles and antiparticles (modeled by consecutive cells with the same state) move in opposite directions and annihilate each other when they collide.

Ballistic annihilation describes a process by which moving particles and antiparticles annihilate each other when they collide. In the simplest version of this process, the system consists of a single type of particle and antiparticle, moving at equal speeds in opposite directions in a one-dimensional medium.

This process can be modeled by Rule 184, as follows. We view the particles as aligned, not with the cells of the automaton, but rather with the interstices between cells. If two consecutive cells both have state 0, we view the transition between them as forming a particle that moves rightwards one cell at each time step. If, on the other hand, two consecutive cells both have state 1, we view the transition between them as forming an antiparticle that moves leftwards one cell at each time step. Two consecutive cells with differing states are considered to form part of a background material without any particles in it. It may be observed that these particles interact by ballistic annihilation: when a rightwards-moving particle and a leftwards-moving antiparticle meet, the result is a region of background from which both particles have vanished, without any effect on any other nearby particles.[15]

The behavior of certain other systems, such as one-dimensional cyclic cellular automata, can also be described in terms of ballistic annihilation.[16] There is a technical restriction on the particle positions for the ballistic annihilation view of Rule 184 that does not arise in these other systems, stemming from the alternating pattern of the background: in the particle system corresponding to a Rule 184 state, if two consecutive particles are both of the same type they must be an odd number of cells apart, while if they are of opposite types they must be an even number of cells apart. However this parity restriction does not play a role in the statistical behavior of this system.

Pivato (2005) uses a similar but more complicated particle-system view of Rule 184: he not only views alternating 0–1 regions as background, but also considers regions consisting solely of a single state to be background as well. Based on this view he describes seven different particles formed by boundaries between regions, and classifies their possible interactions. See Chopard and Droz (1998, pp. 188–190) for a more general survey of the physics of annihilation processes.

Context free parsing

In his book A New Kind of Science, Stephen Wolfram points out that rule 184, when run on patterns with density 50%, can be interpreted as parsing the context free language describing strings formed from nested parentheses. This interpretation is closely related to the ballistic annihilation view of rule 184: in Wolfram's interpretation, an open parenthesis corresponds to a left-moving particle while a close parenthesis corresponds to a right-moving particle.[17]

See also

Notes

  1. ↑ E.g. see Fukś (1997).
  2. ↑ One can find many later papers that, when mentioning Rule 184, cite the early papers of Stephen Wolfram. However, Wolfram's papers consider only automata that are symmetric under left-right reversal, and therefore do not describe Rule 184.
  3. ↑ Li (1992). Li used this interpretation as part of a generalization of Rule 184 to nonlocal neighborhood structures.
  4. ↑ Boccara and Fukś (1998) have investigated more general automata with similar conservation properties, as has Moreira (2003).
  5. ↑ Li (1987).
  6. ↑ Capcarrere et al. (1996); Fukś (1997); Sukumar (1998).
  7. ↑ Land and Belew (1995).
  8. ↑ Nagel (1996); Chowdhury et al. (2000).
  9. ↑ Tadaki and Kikuchi (1994).
  10. ↑ For several models of this type see Nagel and Schreckenberg (1992), Fukui and Ishibashi (1996), and Fukś and Boccara (1998). Nagel (1996) observes the equivalence of these models to rule 184 in the single-speed case and lists several additional papers on this type of model.
  11. ↑ See also Tadaki and Kikuchi (1994) for additional analysis of this model.
  12. ↑ Fukś and Boccara (1998).
  13. ↑ See also Belitzky and Ferrari (1995) and Chopard and Droz (1998, p. 29).
  14. ↑ Also discussed by Krug and Spohn (1988).
  15. ↑ Krug and Spohn (1988); Belitzky and Ferrari (1995).
  16. ↑ Belitzky and Ferrari (1995).
  17. ↑ Wolfram (2002), pp. 989, 1109.

References

External links

Wikimedia Commons has media related to Rule 184.