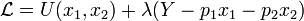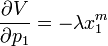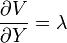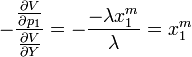Roy's identity
Roy's identity (named for French economist René Roy) is a major result in microeconomics having applications in consumer choice and the theory of the firm. The lemma relates the ordinary (Marshallian) demand function to the derivatives of the indirect utility function. Specifically, where 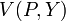 is the indirect utility function, then the Marshallian demand function for good
is the indirect utility function, then the Marshallian demand function for good  can be calculated as:
can be calculated as:
where  is the price vector of goods and
is the price vector of goods and  is income.
is income.
Derivation of Roy's identity
Roy's identity reformulates Shephard's lemma in order to get a Marshallian demand function for an individual and a good ( ) from some indirect utility function.
) from some indirect utility function.
The first step is to consider the trivial identity obtained by substituting the expenditure function for wealth or income  in the indirect utility function
in the indirect utility function 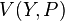 , at a utility of
, at a utility of  :
:
This says that the indirect utility function evaluated in such a way that minimizes the cost for achieving a certain utility given a set of prices (a vector  ) is equal to that utility when evaluated at those prices.
) is equal to that utility when evaluated at those prices.
Taking the derivative of both sides of this equation with respect to the price of a single good 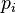 (with the utility level held constant) gives:
(with the utility level held constant) gives:
![\frac{ \partial V [e(u,P),P]}{\partial Y} \frac{\partial e(u,P)}{\partial p_i} + \frac{\partial V [e(u,P),P]}{\partial p_i} = 0](../I/m/d44ba0ebe21bbc5703a07833b62f7514.png) .
.
Rearranging gives the desired result:
Alternative proof for the differentiable case
There is a simpler proof of Roy's identity, stated for the two-good case for simplicity.
The indirect utility function 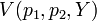 is the maximand of the constrained optimization problem characterized by the following Lagrangian:
is the maximand of the constrained optimization problem characterized by the following Lagrangian:
By the envelope theorem, the derivatives of the maximand 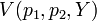 with respect to the parameters can be computed as such:
with respect to the parameters can be computed as such:
where 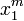 is the maximizer (i.e. the Marshallian demand function for good 1). Simple arithmetic then gives Roy's Identity:
is the maximizer (i.e. the Marshallian demand function for good 1). Simple arithmetic then gives Roy's Identity:
Application
This gives a method of deriving the Marshallian demand function of a good for some consumer from the indirect utility function of that consumer. It is also fundamental in deriving the Slutsky equation.
References
- Roy, René (1947). "La Distribution du Revenu Entre Les Divers Biens". Econometrica 15 (3): 205–225. JSTOR 1905479.
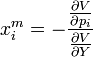
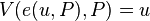
![\frac{\partial e(u,P)}{\partial p_i}=-\frac{\frac{\partial V [e(u,P),P]}{\partial p_i}}{\frac{\partial V [e(u,P),P]}{\partial Y}}=x_i(Y,P)](../I/m/c2d1519101fc3a35e65da29ce984b8ca.png)