Routh–Hurwitz theorem

In mathematics, the Routh–Hurwitz theorem gives a test to determine whether all roots of a given polynomial lie in the left half-plane. Polynomials with this property are called Hurwitz-stable. The Routh–Hurwitz theorem was proved in 1895, and it was named after Edward John Routh and Adolf Hurwitz. It is used in the Routh–Hurwitz stability criterion.

Notations

Let f(z) be a polynomial (with complex coefficients) of degree n with no roots on the imaginary line (i.e. the line Z = ic where i is the imaginary unit and c is a real number). Let us define 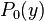$P_0(y)$ (a polynomial of degree n) and 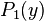$P_1(y)$ (a nonzero polynomial of degree strictly less than n) by 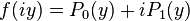$f(iy)=P_0(y)+iP_1(y)$ , respectively the real and imaginary parts of f on the imaginary line.

Furthermore, let us denote by:

p the number of roots of f in the left half-plane (taking into account multiplicities);
q the number of roots of f in the right half-plane (taking into account multiplicities);
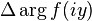$\Delta\arg f(iy)$ the variation of the argument of f(iy) when y runs from −∞ to +∞;
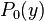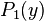'(x) is the number of variations of the generalized Sturm chain obtained from $P_0(y)$ and $P_1(y)$ by applying the Euclidean algorithm;
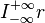$I_{-\infty}^{+\infty}r$ is the Cauchy index of the rational function r over the real line.

Statement

With the notations introduced above, the Routh–Hurwitz theorem states that:

p-q=\frac{1}{\pi}\Delta\arg f(iy)= \left.\begin{cases} +I_{-\infty}^{+\infty}\frac{P_0(y)}{P_1(y)} & \text{for odd degree} \\[10pt] -I_{-\infty}^{+\infty}\frac{P_1(y)}{P_0(y)} & \text{for even degree} \end{cases}\right\} = w(+\infty)-w(-\infty).

From the first equality we can for instance conclude that when the variation of the argument of f(iy) is positive, then f(z) will have more roots to the left of the imaginary axis than to its right. The equality p − q = w(+∞) − w(−∞) can be viewed as the complex counterpart of Sturm's theorem. Note the differences: in Sturm's theorem, the left member is p + q and the w from the right member is the number of variations of a Sturm chain (while w refers to a generalized Sturm chain in the present theorem).

Routh–Hurwitz stability criterion

Main article: Routh–Hurwitz stability criterion

We can easily determine a stability criterion using this theorem as it is trivial that f(z) is Hurwitz-stable iff p − q = n. We thus obtain conditions on the coefficients of f(z) by imposing w(+∞) = n and w(−∞) = 0.

References

Routh, E.J. (1877). A Treatise on the Stability of a Given State of Motion, Particularly Steady Motion. Macmillan and co.
Hurwitz, A. (1964). "On The Conditions Under Which An Equation Has Only Roots With Negative Real Parts". Selected Papers on Mathematical Trends in Control Theory.
Gantmacher, F.R. (1959). "Applications of the Theory of Matrices". Interscience, New York 641 (9): 1–8.
Rahman, Q. I.; Schmeisser, G. (2002). Analytic theory of polynomials. London Mathematical Society Monographs. New Series 26. Oxford: Oxford University Press. ISBN 0-19-853493-0. Zbl 1072.30006.

External links

Mathworld entry