Rouse model

The Rouse model is frequently used in polymer physics.
The Rouse model describes the conformational dynamics of an ideal chain. In this model, the single chain diffusion is represented by Brownian motion of beads connected by harmonic springs. There are no excluded volume interactions between the beads and each bead is subjected to a random thermal force and a drag force as in Langevin dynamics. This model was proposed by Prince E. Rouse in 1953.[1]
An important extension to include hydrodynamic interactions mediated by the solvent between different parts of the chain was worked out by Bruno Zimm in 1956.[2] Whilst the Rouse model overestimates the decrease of the diffusion coefficient D with the number of beads N as 1/N, the Zimm model predicts D~1/Nν which is consistent with the experimental data for dilute polymer solutions (where 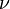 is the Flory exponent).
is the Flory exponent).
In a polymer melt, the Rouse model correctly predicts long-time diffusion only for chains shorter than the entanglement length. For long chains with noticeable entanglement the Rouse model holds only up to a crossover time τe. For longer times the chain can only move within a tube formed by the surrounding chains. This slow motion is usually approximated by the reptation model.
References
- ↑ Prince E. Rouse, A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers, J. Chem. Phys. 21, 1272 (1953), cited over 1000 times by 2010.
- ↑ Bruno H. Zimm, Dynamics of Polymer Molecules in Dilute Solution: Viscoelasticity, Flow Birefringence and Dielectric Loss, J. Chem. Phys. 24, 269 (1956).