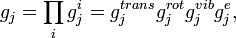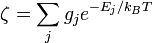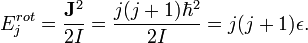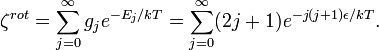Rotational partition function
The rotational partition function relates the rotational degrees of freedom to the rotational part of the energy.
Definition
The total partition function  of a system of identical particles can be divided into molecular partition functions
of a system of identical particles can be divided into molecular partition functions  . Under the assumption that that all energy levels
. Under the assumption that that all energy levels 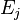 can be partitioned into its contributions from different degrees of freedom (weakly coupled degrees of freedom)
can be partitioned into its contributions from different degrees of freedom (weakly coupled degrees of freedom)
and the number of degenerate states are given as products of the single contributions
where "trans", "rot", "vib" and "e" denotes translational, rotational and vibrational contributions as well as electron excitation, the molecular partition functions
can be written as a product itself
Rotational energies are quantized. For a diatomic molecule like CO or HCl, the allowed rotational energies are
Now 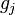 for each level
for each level 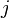 is
is 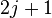 , so the rotational partition function is therefore
, so the rotational partition function is therefore
If the difference between energy levels  is very small compared to
is very small compared to 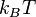 , then the sum can be approximated by an integral and is found to be proportional to the temperature. For more complex polyatomic molecules, the situation is more difficult.
, then the sum can be approximated by an integral and is found to be proportional to the temperature. For more complex polyatomic molecules, the situation is more difficult.
For the CO molecule at  , the (unit less) contribution
, the (unit less) contribution 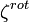 to
to  turns out to be in the range of
turns out to be in the range of 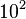 .
.
The rotational energy can now be computed by taking the derivative of 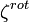 with respect to temperature
with respect to temperature  . This can of course also be done by using the equipartition theorem, which says that in an equilibrium the energies of all degrees of freedom are proportional to the temperature.
. This can of course also be done by using the equipartition theorem, which says that in an equilibrium the energies of all degrees of freedom are proportional to the temperature.
See also
| ||||||||||||||||||||||||||||||||||||||