Rotation map
In mathematics, a rotation map is a function that represents an undirected edge-labeled graph, where each vertex enumerates its outgoing neighbors. Rotation maps were first introduced by Reingold, Vadhan and Wigderson (“Entropy waves, the zig-zag graph product, and new constant-degree expanders”, 2002) in order to conveniently define the zig-zag product and prove its properties.
Given a vertex 
and an edge label 
, the rotation map returns the 'th neighbor of and the edge label that would lead back to .
Definition
For a D-regular graph G, the rotation map ![\mathrm{Rot}_G : [N] \times [D] \rightarrow [N] \times [D]](../I/m/e40c1572d262d61ca053b0a4bf6b6776.png)
is defined as follows: 
if the ith edge leaving v leads to w, and the jth edge leaving w leads to v.
Basic properties
From the definition we see that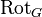 
is a permutation, and moreover 
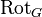is the identity map ( is an involution).
Special cases and properties
- A rotation map is consistently labeled if all of the edges leaving each vertex are labeled in such a way that at each vertex, the labels of the incoming edges are all distinct. Every regular graph has some consistent labeling.
- A rotation map is
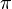-consistent if ![\forall v \ \mathrm{Rot}_G(v,i)=(v[i],\pi (i))](../I/m/2da654fc46c71333fc17cd5c120de3f1.png)
. From the definition, a 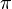-consistent rotation map is consistently labeled.
See also
References
- Reingold, O.; Vadhan, S.; Widgerson, A. (2000), "Entropy waves, the zig-zag graph product, and new constant-degree expanders and extractors", 41st Annual Symposium on Foundations of Computer Science: 3–13, doi:10.1109/SFCS.2000.892006
- Reingold, O (2008), "Undirected connectivity in log-space", Journal of the ACM 55 (4): Article 17, 24 pages, doi:10.1145/1391289.1391291
- Reingold, O.; Trevisan, L.; Vadhan, S. (2006), "Pseudorandom walks on regular digraphs and the RL vs. L problem", Proceedings of the thirty-eighth annual ACM symposium on Theory of computing: 457, doi:10.1145/1132516.1132583