Rossby radius of deformation

In atmospheric dynamics and physical oceanography, the Rossby radius of deformation is the length scale at which rotational effects become as important as buoyancy or gravity wave effects in the evolution of the flow about some disturbance.^[1]

For a barotropic ocean: 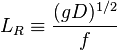$L_R \equiv \frac{(gD)^{1/2}}{f}$ , where 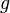$\,g$ is the gravitational acceleration, 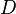$\,D$ is the water depth, and 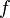$\,f$ is the Coriolis parameter.^[2]

For f = 1×10⁻⁴ s⁻¹ appropriate to 45° latitude, and D = 4 km, L_R ≈ 2000 km; and for D = 40 m, L_R ≈ 200 km.

The nth baroclinic Rossby radius is:

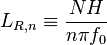L_{R, n} \equiv \frac{NH}{n \pi f_0}

, where

\,N

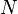is the Brunt–Väisälä frequency,

\,H

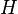is the scale height, and n = 1, 2, ....

In Earth's atmosphere, the ratio N/f₀ is typically of order 100, so the Rossby radius is about 100 times the vertical scale height, H. For a vertical scale associated with the height of the tropopause, L_{R, 1} ≈ 1000 km, which is the predominant scale seen on weather charts for cyclones and anticyclones. This is commonly called the synoptic scale.

The associated dimensionless parameter is the Rossby number. Both are named in honor of Carl-Gustav Rossby.

References

↑ Gill, A. E., 1982: Atmosphere-Ocean Dynamics, Academic Press, Orlando, 662 pp.
↑ Cushman-Roisin, B. & Beckers, J.M., 2011: Introduction to Geophysical Fluid Dynamics, Academic Press, Waltman, p. 275