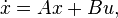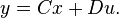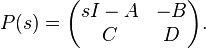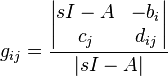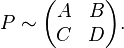Rosenbrock system matrix
The Rosenbrock System Matrix (or Rosenbrock's system matrix) of a linear time invariant system is a useful representation bridging state-space representation and transfer function matrix form. It was proposed in 1967 by Howard H. Rosenbrock.[1]
Definition
Consider the dynamic system
The Rosenbrock system matrix is given by
In the original work by Rosenbrock, the constant matrix 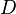 is allowed to be a polynomial in
is allowed to be a polynomial in  .
.
The transfer function between the input 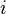 and output
and output 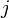 is given by
is given by
where 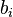 is the column
is the column 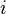 of
of 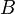 and
and 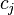 is the row
is the row 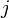 of
of  .
.
Based in this representation, Rosenbrock developed his version of the PHB test.
Short form
For computational purposes, a short form of the Rosenbrock system matrix is more appropriate[2] and given by
The short form of the Rosenbrock system matrix has been widely used in H-infinity methods in control theory, where it is also referred to as packed form; see command pck in.[3] An interpretation of the Rosenbrock System Matrix as a Linear Fractional Transformation can be found in.[4]
One of the first applications of the Rosenbrock form was the development of an efficient computational method for Kalman decomposition, which is based on the pivot element method. A variant of Rosenbrock’s method is implemented in the minreal command of Matlab.[5] as well as GNU Octave.
References
- ↑ Rosenbrock, H.H. (1967). "Transformation of linear constant system equations". Proc. I.E.E. 114: 541–544.
- ↑ Rosenbrock, H. H. (1970). State-Space and Multivariable Theory. Nelson.
- ↑ "Mu Analysis and Synthesis Toolbox". Retrieved 25 August 2014.
- ↑ Zhou, Kemin; Doyle, John C.; Glover, Keith (1995). Robust and Optimal Control. Prentice Hall.
- ↑ De Schutter, B. (2000). "Minimal state-space realization in linear system theory: an overview". Journal of Computational and Applied Mathematics 121 (1-2): 331–354. doi:10.1016/S0377-0427(00)00341-1.