Rosati involution
In mathematics, a Rosati involution, named after Carlo Rosati, is an involution of the rational endomorphism ring of an abelian variety induced by a polarization.
Let 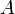 be an abelian variety, let
be an abelian variety, let 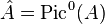 be the dual abelian variety, and for
be the dual abelian variety, and for 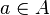 , let
, let 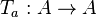 be the translation-by-
be the translation-by-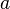 map,
map, 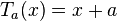 . Then each divisor
. Then each divisor 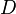 on
on 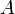 defines a map
defines a map 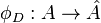 via
via ![\phi_D(a)=[T_a^*D-D]](../I/m/a5491f6040e0cb32a01b775df1e25022.png) . The map
. The map 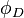 is a polarization, i.e., has finite kernel, if and only if
is a polarization, i.e., has finite kernel, if and only if 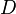 is ample. The Rosati involution of
is ample. The Rosati involution of 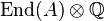 relative to the polarization
relative to the polarization 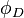 sends a map
sends a map 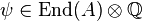 to the map
to the map 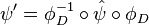 , where
, where 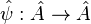 is the dual map induced by the action of
is the dual map induced by the action of 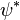 on
on 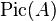 .
.
Let 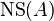 denote the Néron–Severi group of
denote the Néron–Severi group of 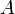 . The polarization
. The polarization 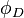 also induces an inclusion
also induces an inclusion 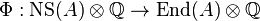 via
via 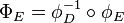 . The image of
. The image of 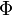 is equal to
is equal to 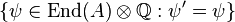 , i.e., the set of endomorphisms fixed by the Rosati involution. The operation
, i.e., the set of endomorphisms fixed by the Rosati involution. The operation 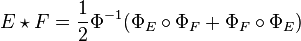 then gives
then gives 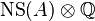 the structure of a formally real Jordan algebra.
the structure of a formally real Jordan algebra.
References
- Mumford, David (2008) [1970], Abelian varieties, Tata Institute of Fundamental Research Studies in Mathematics 5, Providence, R.I.: American Mathematical Society, ISBN 978-81-85931-86-9, MR 0282985, OCLC 138290
- Rosati, Carlo (1918), "Sulle corrispondenze algebriche fra i punti di due curve algebriche.", Annali di Matematica Pura ed Applicata (in Italian) 3 (28): 35–60, doi:10.1007/BF02419717