Root datum
In mathematical group theory, the root datum (donnée radicielle in French) of a connected split reductive algebraic group over a field is a generalization of a root system that determines the group up to isomorphism. They were introduced by Michel Demazure in SGA III, published in 1970.
Definition
A root datum consists of a quadruple
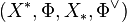 ,
,
where
-
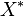 and
and 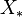 are free abelian groups of finite rank together with a perfect pairing between them with values in
are free abelian groups of finite rank together with a perfect pairing between them with values in 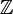 which we denote by ( , ) (in other words, each is identified with the dual lattice of the other).
which we denote by ( , ) (in other words, each is identified with the dual lattice of the other). -
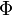 is a finite subset of
is a finite subset of 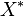 and
and 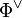 is a finite subset of
is a finite subset of 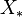 and there is a bijection from
and there is a bijection from 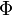 onto
onto 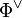 , denoted by
, denoted by 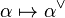 .
. - For each
 ,
, 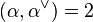 .
. - For each
 , the map
, the map 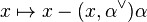 induces an automorphism of the root datum (in other words it maps
induces an automorphism of the root datum (in other words it maps 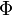 to
to 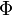 and the induced action on
and the induced action on 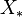 maps
maps 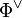 to
to 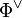 )
)
The elements of 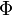 are called the roots of the root datum, and the elements of
are called the roots of the root datum, and the elements of 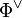 are called the coroots. The elements of
are called the coroots. The elements of 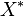 are sometimes called weights and those of
are sometimes called weights and those of 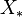 accordingly coweights.
accordingly coweights.
If 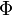 does not contain
does not contain 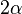 for any
for any 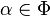 , then the root datum is called reduced.
, then the root datum is called reduced.
The root datum of an algebraic group
If G is a reductive algebraic group over an algebraically closed field K with a split maximal torus T then its root datum is a quadruple
- (X*, Φ, X*, Φv),
where
- X* is the lattice of characters of the maximal torus,
- X* is the dual lattice (given by the 1-parameter subgroups),
- Φ is a set of roots,
- Φv is the corresponding set of coroots.
A connected split reductive algebraic group over K is uniquely determined (up to isomorphism) by its root datum, which is always reduced. Conversely for any root datum there is a reductive algebraic group. A root datum contains slightly more information than the Dynkin diagram, because it also determines the center of the group.
For any root datum (X*, Φ,X*, Φv), we can define a dual root datum (X*, Φv,X*, Φ) by switching the characters with the 1-parameter subgroups, and switching the roots with the coroots.
If G is a connected reductive algebraic group over the algebraically closed field K, then its Langlands dual group LG is the complex connected reductive group whose root datum is dual to that of G.
References
- Michel Demazure, Exp. XXI in SGA 3 vol 3
- T. A. Springer, Reductive groups, in Automorphic forms, representations, and L-functions vol 1 ISBN 0-8218-3347-2