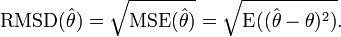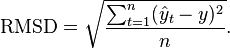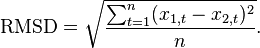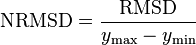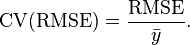Root-mean-square deviation
The root-mean-square deviation (RMSD) or root-mean-square error (RMSE) is a frequently used measure of the differences between values (sample and population values) predicted by a model or an estimator and the values actually observed. Basically, the RMSD represents the sample standard deviation of the differences between predicted values and observed values. These individual differences are called residuals when the calculations are performed over the data sample that was used for estimation, and are called prediction errors when computed out-of-sample. The RMSD serves to aggregate the magnitudes of the errors in predictions for various times into a single measure of predictive power. RMSD is a good measure of accuracy, but only to compare forecasting errors of different models for a particular variable and not between variables, as it is scale-dependent.[1]
Formula
The RMSD of an estimator 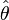 with respect to an estimated parameter
with respect to an estimated parameter  is defined as the square root of the mean square error:
is defined as the square root of the mean square error:
For an unbiased estimator, the RMSD is the square root of the variance, known as the standard error.
The RMSD of predicted values 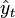 for times t of a regression's dependent variable
for times t of a regression's dependent variable  is computed for n different predictions as the square root of the mean of the squares of the deviations:
is computed for n different predictions as the square root of the mean of the squares of the deviations:
In some disciplines, the RMSD is used to compare differences between two things that may vary, neither of which is accepted as the "standard". For example, when measuring the average difference between two time series 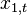 and
and 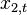 ,
the formula becomes
,
the formula becomes
Normalized root-mean-square deviation
Normalizing the RMSD facilitates the comparison between datasets or models with different scales. Though there is no consistent means of normalization in the literature, the range of the measured data defined as the maximum value minus the minimum value is a common choice:[2]
This value is commonly referred to as the normalized root-mean-square deviation or error (NRMSD or NRMSE), and often expressed as a percentage, where lower values indicate less residual variance.
Another common choice is to normalize by the mean value of the measurements:[3]
When the RMSD is normalized by the mean measured value, is usually called coefficient of variation of the RMSE, CV(RMSE). It is analogous to the coefficient of variation with the RMSE taking the place of the standard deviation.
Applications
- In meteorology, to see how effectively a mathematical model predicts the behavior of the atmosphere
- In bioinformatics, the RMSD is the measure of the average distance between the atoms of superimposed proteins.
- In structure based drug design, the RMSD is a measure of the difference between a crystal conformation of the ligand conformation and a docking prediction.
- In economics, the RMSD is used to determine whether an economic model fits economic indicators. Some experts have argued that RMSD is less reliable than Relative Absolute Error.[4]
- In experimental psychology, the RMSD is used to assess how well mathematical or computational models of behavior explain the empirically observed behavior.
- In GIS, the RMSD is one measure used to assess the accuracy of spatial analysis and remote sensing.
- In hydrogeology, RMSD and NRMSD are used to evaluate the calibration of a groundwater model.[5]
- In imaging science, the RMSD is part of the peak signal-to-noise ratio, a measure used to assess how well a method to reconstruct an image performs relative to the original image.
- In computational neuroscience, the RMSD is used to assess how well a system learns a given model.[6]
- In Protein nuclear magnetic resonance spectroscopy, the RMSD is used as a measure to estimate the quality of the obtained bundle of structures.
- Submissions for the Netflix Prize were judged using the RMSD from the test dataset's undisclosed "true" values.
- In simulation of energy consumption of buildings, the RMSE and CV(RMSE) are used to calibrate models to measured building performance.
See also
References
- ↑ Hyndman, Rob J. Koehler, Anne B.; Koehler (2006). "Another look at measures of forecast accuracy". International Journal of Forecasting 22 (4): 679–688. doi:10.1016/j.ijforecast.2006.03.001.
- ↑ "Coastal Inlets Research Program (CIRP) Wiki - Statistics". Retrieved 4 February 2015.
- ↑ "FAQ: What is the coefficient of variation?". Retrieved 4 February 2015.
- ↑ J. Scott Armstrong and Fred Collopy (1992). "Error Measures For Generalizing About Forecasting Methods: Empirical Comparisons". International Journal of Forecasting 8 (1): 69–80. doi:10.1016/0169-2070(92)90008-w.
- ↑ Anderson, M.P.; Woessner, W.W. (1992). Applied Groundwater Modeling: Simulation of Flow and Advective Transport (2nd ed.). Academic Press.
- ↑ Ensemble Neural Network Model