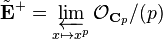Fontaine's period rings
In mathematics, Fontaine's period rings are a collection of commutative rings first defined by Jean-Marc Fontaine that are used to classify p-adic Galois representations.
The ring BdR
The ring 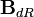 is defined as follows. Let
is defined as follows. Let 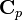 denote the completion of
denote the completion of 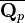 . Let
. Let
So an element of 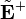 is a sequence
is a sequence 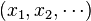 of elements
of elements
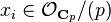 such that
such that 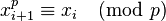 . There is a natural projection map
. There is a natural projection map 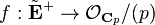 given by
given by 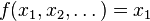 . There is also a multiplicative (but not additive) map
. There is also a multiplicative (but not additive) map 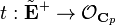 defined by
defined by 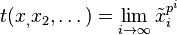 , where the
, where the 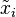 are arbitrary lifts of the
are arbitrary lifts of the 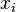 to
to 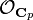 . The composite of
. The composite of 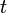 with the projection
with the projection 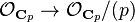 is just
is just  . The general theory of Witt vectors yields a unique ring homomorphism
. The general theory of Witt vectors yields a unique ring homomorphism 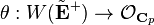 such that
such that ![\theta([x]) = t(x)](../I/m/7b31ce5c31cd2998d3f259f0ed6832ba.png) for all
for all 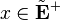 , where
, where ![[x]](../I/m/3e5314e9fd31509fdeb83faa0f729ba2.png) denotes the Teichmüller representative of
denotes the Teichmüller representative of 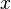 . The ring
. The ring 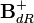 is defined to be completion of
is defined to be completion of ![\tilde{\mathbf{B}}^+ = W(\tilde{\mathbf{E}}^+)[1/p]](../I/m/fbd20d4a6607d524bc9ef31406079c41.png) with respect to the ideal
with respect to the ideal 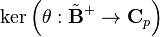 . The field
. The field 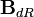 is just the field of fractions of
is just the field of fractions of 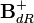 .
.
References
Secondary sources
- Berger, Laurent (2004), "An introduction to the theory of p-adic representations", Geometric aspects of Dwork theory I, Berlin: Walter de Gruyter GmbH & Co. KG, arXiv:math/0210184, ISBN 978-3-11-017478-6, MR 2023292
- Brinon, Olivier; Conrad, Brian (2009), CMI Summer School notes on p-adic Hodge theory, retrieved 2010-02-05
- Fontaine, Jean-Marc, ed. (1994), Périodes p-adiques, Astérisque 223, Paris: Société Mathématique de France, MR 1293969