Ring laser

Ring lasers are composed of two beams of light of the same polarization traveling in opposite directions ("counter-rotating") in a closed loop.

Currently ring lasers are used most frequently as gyroscopes (ring laser gyroscope; (figure 2)) in moving vessels like cars, ships, planes, and missiles. The world's largest ring lasers can detect details of the Earth's rotation. Such large rings are also capable of extending scientific research in many new directions, including the detection of gravitational waves, Fresnel drag, Lense-Thirring effect, and quantum-electrodynamic effects (see Ring Lasers for Research).

In a rotating ring laser gyroscope, the two counter-propagating waves are slightly shifted in frequency and an interference pattern is observed, which is used to determine the rotational speed. The response to a rotation is a frequency difference between the two beams, which is proportional ^[1] to the rotation rate of the ring laser (Sagnac effect). The difference can easily be measured. Generally however, any non reciprocity in the propagation between the two beams leads to a beat frequency.

Engineering applications

There is a continuous transition between ring lasers for engineering application and ring lasers for research (see Ring Lasers for Research). Rings for engineering have begun to incorporate a vast variety of materials as well as new technology. Historically, the first extension was the use of fiber optics as wave guides, obviating the use of mirrors. However, even rings using the most advanced fiber working in its optimal wavelength range (e.g. SiO₂ at 1.5 μm) have vastly higher losses than square rings with four high-quality mirrors. Therefore, fiber optic rings suffice only in high rotation rate applications. For example, fiber optic rings are now common in automobiles.

Figure 2.Commercial Ring Laser Gyro encased in quartz.

A ring can be constructed with other optically active materials that are able to conduct a beam with low losses. One type of ring laser design is a single crystal design, where light reflects around inside the laser crystal so as to circulate in a ring. This is the "monolithic crystal" design, and such devices are known as "non-planar ring oscillators" (NPROs) or MISERs.^[2] There are also ring fiber lasers.^[3]^[4] Since typically the achievable quality factors are low, such rings cannot be used for research where quality factors above 10¹² are sought and are achievable.

History

Table 1. ~10⁸ improvement in the resolution of large rings from 1972 to 2004.
year	rms linewidth	measurement time	source
1972	4.5 Hz	10 s	Stowell
1993	68 mHz	16 s	Bilger
1994	31 mHz	8 h	Stedman
1996	8.6 µHz	8 d	Bilger
2004	50 nHz	243 d	Schreiber

Shortly after the discovery of the laser, a seminal paper by Rosenthal appeared in 1962,^[5] which proposed what was later called a ring laser. While the ring laser shares with regular (linear) lasers features like extreme monochromaticity and high directivity, it differs in its inclusion of an area. With the ring laser, one could distinguish two beams in opposite directions. Rosenthal anticipated that the beam frequencies could be split by effects that affected the two beams in different ways. Although some may consider Macek et al. has built the first large ring laser (1 meter × 1 meter).^[6] The US patent office has decided the first ring laser was built under Sperry scientist, Chao Chen Wang, (see US Patent 3,382,758) based on the Sperry laboratory records. Wang showed that simply rotating it could generate a difference in the frequencies of the two beams (Sagnac^[7]). An industry focusing on smaller ring laser gyros emerged, with decimeter-sized ring lasers. Later it was found that any effect that affects the two beams in nonreciprocal fashion produces a frequency difference, as Rosenthal anticipated. Tools to analyze and construct rings were adapted from regular lasers, including methods to calculate the signal-to-noise ratio and to analyze beam characteristics. New phenomena unique to rings appeared, including lock-in, pulling, astigmatic beams, and special polarizations. Mirrors play a much greater role in ring lasers than in linear lasers, leading to the development of particularly high quality mirrors.

The resolution of large ring lasers has dramatically improved, as a result of a 1000-fold improvement in the quality factor (see Table 1). This improvement is largely a result of the removal of interfaces that the beams need to traverse as well as the improvements on technology which allowed a dramatic increase in measurement time (see section on Line Width). A 1 m × 1 m ring built in Christchurch, New Zealand in 1992^[8] was sensitive enough to measure the Earth's rotation (figure 3), and a 4 m × 4 m ring built in Wettzell, Germany improved the precision of this measurement to six digits^[9] (figure 4).

Figure 3. The Canterbury ring, built in 1992.

Figure 4. Grossring in Wettzell, Germany, built by Zeiss (Oberkochen, Germany).

Construction

In ring lasers, mirrors are used to focus and redirect the laser beams at the corners. While traveling between mirrors, the beams pass through gas-filled tubes. The beams are generally generated through local excitation of the gas by radio frequencies.

Critical variables in the construction of a ring laser include:

1. Size: Larger ring lasers can measure lower frequencies. The sensitivity of large rings increases quadratically with size.

2. Mirrors: High reflectivity is important.

3. Stability: The assembly must be attached to or built within a substance that changes minimally in response to temperature fluctuations (e.g. Zerodur, or bedrock for extremely large rings).

4. Gas: HeNe generates beams with the most desirable features for large ring lasers. For gyros, in principle any material that can be used to generate monochromatic light beams is applicable.

The laser beam: theoretical tools

For a ring as a measuring tool, Signal/Noise ratio and line widths are all-important. The signal of the ring as a rotation detector is used, whereas the all-pervasive white, quantum noise is the fundamental noise of the ring. Rings with a low quality factor generate additional low frequency noise.^[10] The standard matrix methods for the beam characteristics — curvature and width — are given, as well as the Jones calculus for polarization.

Signal-to-noise ratio

The following equations can be used to calculate the signal-to-noise ratio, S/N for rotation.

The signal frequency is

S = Δfs = 4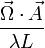 $\frac{\vec{\Omega }\cdot \vec{A}}{\lambda L}$ ,

where 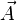$\vec{A}$ is the area vector, 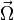$\vec{\Omega }$ is the rotation rate vector, λ is the vacuum wavelength, L is the perimeter. (For complicated geometries like nonplanar rings ^[11] or figure-8 rings,^[12] the definitions

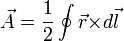$\vec{A}=\frac{1}{2}\oint{\vec{r}\times}d\vec{l}$ and L = 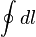$\oint{dl}$ are to be used.)

The noise frequencies are ^[13]

N = 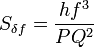$S_{\delta f}=\frac{hf^{3}}{PQ^{2}}$ ,

where 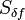$S_{\delta f}$ is the one-sided power spectral density of quantum noise, h is Planck’s constant, f is the laser frequency, P includes all power losses of the laser beams, and Q is the quality factor of the ring.

Line width

Ring Lasers serve as frequency measuring devices. As such, single Fourier components, or lines in frequency space are of major importance in ring outputs. Their widths are determined by the prevailing noise spectra. The major noise contribution is typically white quantum noise ^[13] If this noise is the only one present, the rms-line width sigma is obtained by corrupting the signal (represented by a δ function) with this noise in the interval 0-T. The result is:

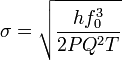
$\sigma =\sqrt{\frac{hf_{0}^3}{2PQ^2T}}$

P should be maximized but kept below the level that generates additional modes. Q can largely be increased by avoiding losses (e.g. improving the quality of the mirrors). T is only limited by the stability of the device. T reduces the line width by the classic T^−1/2 for white noise.

For low-Q rings, an empirical relation for 1/f noise has been ascertained, with the one-sided frequency power spectral density given by 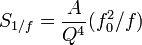$S_{1/f}=\frac{A}{Q^{4}}(f_{0}^2/f)$ , with A≃4. It is notoriously difficult to reduce line width in the presence of this noise.

To decrease the line width further, long measurement times are necessary. A measurement time of 243 days reduced the σ to 50 nHz in the Grossring.

Beam characteristics

The beam in ring lasers is typically excited by High-Frequency excitation of a laser gas. Although it has been shown that ring lasers can be excited in all kinds of modes, including microwave-related modes, a typical ring laser mode has a Gaussian, closed shape, given proper adjustment of mirror position ^[14] The analysis of beam properties (curvature radius, width, position of waists, polarization) is done with matrix methods, where the elements of the closed beam circuit, mirrors and distances in between, are given 2 × 2 matrices. The results are distinct for circuits with n mirrors. Typically, there are n waists. For stability, there has to be at least one curved mirror in the circuit. Out-of-plane rings have circular polarization. The choice of mirror radii and mirror separation is not arbitrary.

Curvature radius and width

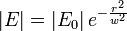The beam has a spot size w: $\left| E \right|=\left| E_{0} \right|e^{-\frac{r^{2}}{w^{2}}}$ ,

where 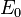$E_{0}$ is the peak field of the beam, E is the field distribution, and r is the distance off beam center.

The mirror sizes have to be chosen large enough to ensure that only very small portions of the gaussian tails are to be cut off, such that the calculated Q (below) is maintained.

The phase is spherical with radius of curvature R. It is customary to combine radius of curvature and spot size into a complex curvature

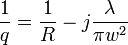$\frac{1}{q}=\frac{1}{R}-j\frac{\lambda }{\pi w^{2}}$ .

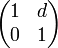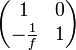The ring design uses a matrix M₁ = $\left( \begin{matrix} 1 & d \\ 0 & 1 \\ \end{matrix} \right)$ for a straight section and M₂ = $\left( \begin{matrix} 1 & 0 \\ -\frac{1}{f} & 1 \\ \end{matrix} \right)$ for a mirror of focus length f. The relation between mirror radius R_M and focus length f is for oblique incidence at angle θ, in plane:

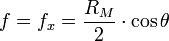$f=f_{x}=\frac{R_{M}}{2}\cdot \cos \theta$ ,

for oblique incidence at angle θ, perpendicular to the plane:

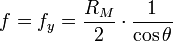$f=f_{y}=\frac{R_{M}}{2}\cdot \frac{1}{\cos \theta }$ ,

resulting in astigmatic beams.

The matrices have

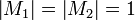$\left| M_{1} \right|=\left| M_{2} \right|=1$ .

A typical design of a rectangular ring has the following form:

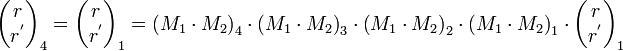
$\left( \begin{matrix} r \\ r^{'} \\ \end{matrix} \right)_{4}=\left( \begin{matrix} r \\ r^{'} \\ \end{matrix} \right)_{1}=\left( M_{1}\cdot M_{2} \right)_{4}\cdot \left( M_{1}\cdot M_{2} \right)_{3}\cdot \left( M_{1}\cdot M_{2} \right)_{2}\cdot \left( M_{1}\cdot M_{2} \right)_{1}\cdot \left( \begin{matrix} r \\ r^{'} \\ \end{matrix} \right)_{1}$

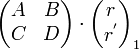
$\left( \begin{matrix} A & B \\ C & D \\ \end{matrix} \right)\cdot \left( \begin{matrix} r \\ r^{'} \\ \end{matrix} \right)_{1}$

(for the equivalent rays where r = distance of equivalent ray from the axis, r’ = the slope against the axis).

Note that in order for the ray to close on itself, the input column matrix has to equal the output column. This round-trip matrix is actually called ABCD matrix in the literature.^[14]

The requirement that the ray is to be closed is therefore 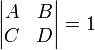$\left| \begin{matrix} A & B \\ C & D \\ \end{matrix} \right|=1$ .

Propagation of complex curvature

The complex curvatures q_in and q_out in a section of a beam circuit with the section matrix 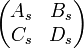$\left( \begin{matrix} A_{s} & B_{s} \\ C_{s} & D_{s} \\ \end{matrix} \right)$ is

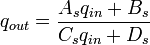$q_{out}=\frac{A_sq_{in}+B_s}{C_sq_{in}+D_s}$ . In particular, if the matrix above is the round-trip matrix, the q at that point is

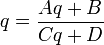$q=\frac{Aq+B}{Cq+D}$ ,

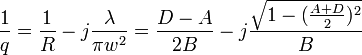$\frac{1}{q}=\frac{1}{R}-j\frac{\lambda }{\pi w^{2}}=\frac{D-A}{2B}-j\frac{\sqrt{1-(\frac{A+D}{2})^{2}}}{B}$ .

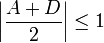
Note that it is necessary that $\left| \frac{A+D}{2} \right|\le 1$

to have a real spot size (Stability Criterion). The width is generally less than 1 mm for small lasers, but it increases approximately with 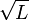$\sqrt{L}$ . For calculation of beam positions for misaligned mirrors, see ^[15]

Polarization

The polarization of rings exhibits particular features: Planar rings are either s-polarized, i.e. perpendicular to the ring plane, or p-polarized, in the plane; non-planar rings are circularly polarized. The Jones calculus^[14] is used to calculate polarization. Here, the column matrix

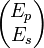
$\left( \begin{matrix} E_{p} \\ E_{s} \\ \end{matrix} \right)$

signifies the electric field components in-plane and off-plane. To study further the transition from planar rings to non-planar rings,^[16] reflected amplitudes r_p and r_s as well as phase shifts upon mirror reflection χ_p and χ_s are introduced in an extended mirror matrix

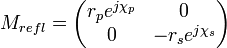$M_{refl}=\left( \begin{matrix} r_{p}e^{j\chi _{p}} & 0 \\ 0 & -r_{s}e^{j\chi _{s}} \\ \end{matrix} \right)$ . Also, if the reference planes change, one needs to refer the E-vector after reflection to the new planes with the rotation matrix

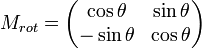$M_{rot}=\left( \begin{matrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \\ \end{matrix} \right)$ .

Analysis of a skew-square ring by the Jones calculus yields the polarization in a ring. (A skew-square ring is a plane square ring where one mirror is lifted out of the plane of the other mirrors by a (dihedral) angle θ and tilted accordingly.) Following the Jones’ vector around the closed circuit, one gets

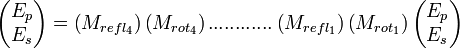$\left( \begin{matrix} E_{p} \\ E_{s} \\ \end{matrix} \right)=\left( M_{refl_{4}} \right)\left( M_{rot_{4}} \right)............\left( M_{refl_{1}} \right)\left( M_{rot_{1}} \right)\left( \begin{matrix} E_{p} \\ E_{s} \\ \end{matrix} \right)$ (Note that the polarization at the end of the loop has to equal the polarization at the start). For small loss differences 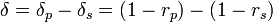$\delta =\delta _{p}-\delta _{s}=(1-r_{p})-(1-r_{s})$ and small phase shift differences 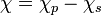$\chi =\chi _{p}-\chi _{s}$ , the solution for 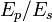$E_{p}/E_{s}$ is

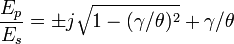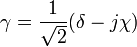$\frac{E_{p}}{E_{s}}=\pm j\sqrt{1-(\gamma /\theta )^{2}}+\gamma /\theta$ , where $\gamma =\frac{1}{\sqrt{2}}(\delta -j\chi )$ . If the dihedral angle θ is large enough, i.e. if

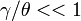$\gamma /\theta <<1$ , the solution of this equation is simply 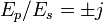$E_{p}/E_{s}=\pm j$ , i.e. a definitely non-planar beam is (left-handed or right-handed) circularly (not elliptically) polarized. On the other hand, if 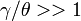$\gamma /\theta >>1$ (a planar ring), the formula above results in p or s reflection (linear polarization). A planar ring, however, is invariably s-polarized because the losses of the multilayer mirrors used are always less in s-polarized beams (at the so-called “Brewster angle”, the reflected p-component even vanishes). There are at least two interesting applications:

1. The Raytheon ring laser. The fourth mirror is elevated by a certain amount over the plane of the other three. The Raytheon ring laser works with four circular polarizations, where now the difference of the differences represents twice the Sagnac effect. This configuration is in principle insensitive to drift. The scheme of detection is also more immune to stray light etc. Raytheon’s use of a Faraday element to split internal frequencies introduces however optical 1/f noise and renders the device non-optimal as a gyro.

2. If the fourth mirror is suspended such that it can rotate around a horizontal axis, the appearance of 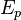$E_{p}$ is extremely sensitive to the mirror’s rotation. In a reasonable arrangement, an angular sensitivity of ±3 picoradian or 0.6 microarcsecond is estimated. With a mass suspended on the rotatable mirror, a simple gravitational wave detector can be constructed.

Lock-in and pulling

These are new phenomena in rings. The lock-in frequency f_L, is the frequency at which the difference between the beam frequencies becomes so small that it collapses, synchronizing the two counterrotating beams. Generally, if the theoretical frequency difference is f_t, the actual signal frequency f is

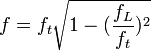$f=f_{t}\sqrt{1-(\frac{f_{L}}{f_{t}})^{2}}$ . This equation says that even slightly above lock-in, there is already a reduction in frequency (i.e. pulling) relative to the theoretical frequency. In the presence of several satellites, only the major signal is pulled. The other satellites have their proper, non-pulled, frequency separation from the major signal. This opens the way to classic precision side-band spectroscopy as is known in microwaves, except that the ring laser has side bands down to nHz.

When the dependence on perimeter L is taken into account for large rings, the relative difference between theoretical output frequency f_t and actual output frequency f is inversely proportional to the fourth power of L:

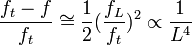$\frac{f_{t}-f}{f_{t}}\cong \frac{1}{2}(\frac{f_{L}}{f_{t}})^{2}\propto \frac{1}{L^{4}}$ .

This is a huge advantage of large rings over small ones. As an example, small navigational gyros have lock-in frequencies on the order of 1 kHz. The first large ring^[6] had a lock-in frequency of about 2 kHz, and the first ring that could measure the Earth’s rotation rate had a lock-in frequency of about 20 Hz.

The cavity

The quality factor Q of the cavity, as well as the time duration of the measurement, determines the achievable frequency resolution of a ring to a large extent. The quality factor depends largely on the reflection properties of the mirrors. For high quality rings, reflectivities larger than 99.999% (R = 1-10 ppm) are indispensable. At this time, the main limitation of mirrors is the extinction coefficient of the evaporated high-index material TiO₂. The size and shape of the cavity as well as the presence of interfaces also influence the quality factor.

Quality factor Q

It is quite important for large rings to increase the quality factor Q, because it appears as 1/Q² in the expression for noise.

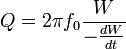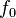Definition of Q: $Q=2\pi f_{0}\frac{W}{-\frac{dW}{dt}}$ . Since the operating frequency $f_{0}$ of the ring is given (474 THz), it remains to increase the circulating energy in the ring W and decrease the power losses dW/dt as much as possible. W is obviously proportional to the length of the ring, but must be limited to avoid multimodes. The power losses dW/dt however can be vastly decreased. The ensuing decreased signal output power is not critical, as modern silicon detectors have low noise, and for very low signals photomultipliers are used.

The power loss can be minimized by increasing the reflectivity of the mirrors to as close to 1 as possible and by eliminating other, spurious, sources of power loss, for example the inaccuracy of mirror curvature. Any interfaces or apertures that would decrease the quality factor of the ring are avoided. The whole ring is filled with a HeNe mixture of suitable partial pressures (up to a few hundred Pascal), to achieve lasing and good suppression of multiple pairs of modes. (Typically, the HeNe lasing gas at 633 nm is used; attempts for an argon ring laser failed.^[17]) Further, the lasing is excited with radio frequency to easily adjust the amplitude to just below the appearance of the second pair of modes. The Rayleigh scattering of the HeNe gas is, at this time, negligible.

For mirrors of proper curvature (spherical shape is acceptable) and equal reflectances r, the quality factor is

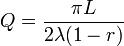$Q=\frac{\pi L}{2\lambda (1-r)}$ .

This equation gives rise to formidable quality factors. For a 4 m x 4 m ring equipped with 1 ppm mirrors (R = 1-10⁻⁶) we would get, at 474 THz, Q = 4×10¹³. This quality factor produces a passive resonance line of rms = 5 Hz, which is eight orders of magnitude smaller than the atomic linewidth of the Ne line (a 1:1 mixture of the two isotopes 20
Ne and 22
Ne has a gain bandwidth of about 2.2 GHz^[11]). (Note that for example in regular pendulums the Q is of the order of 10³ and in wristwatch-type quartzes it is of the order of 10⁶.) The active ring further reduces the linewidth by several orders of magnitude, and increasing the measuring time may additionally decrease the linewidth by many orders of magnitude.

Measurement

The integral of the definition equation for Q above is: 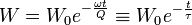$W=W_{0}e^{-\frac{\omega t}{Q}}\equiv W_{0}e^{-\frac{t}{\tau }}$ (τ is the photon lifetime.) Thus, Q = ωτ. This is an extremely simple equation to measure Q in large rings. The photon lifetime τ is measured on an oscilloscope, as the times are of the order of microseconds to milliseconds.

Shape of rings

In order to maximize the signal/noise ratio of a ring inside a given circle of radius r with n mirrors, a planar ring is advantageous over an equivalent nonplanar ring. Furthermore, a regular polygon has a maximal A/Ln ratio, with A/Ln = 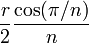$\frac{r}{2}\frac{\cos (\pi /n)}{n}$ which itself has a maximum at n = 4, hence a planar square ring is optimal.

Mirrors

It is essential for a high quality ring to use mirrors of very high reflectivity. Metallic mirror surfaces are inadequate for laser work (household Al-covered mirror surfaces are 83% reflective, Ag is 95% reflective). However, multilayer dielectric mirrors with 20–30 alternate (low L and high H index of refraction) SiO
2 — TiO
2 λ/4 layers achieve reflection losses (1 - r) of single parts per million, and an analysis ^[18] shows that losses of parts per billion can be achieved, if materials technology ^[19] is pushed as far as is done with fiber optics.

The losses are composed of scattering S, absorption A, and transmission T, such that 1 - r = S + A + T. Scattering is not treated here, because it is largely dependent on details of surface and interface treatment, and not easily analyzed.^[19]

r, A, and T are amenable to analysis. The losses are analyzed with a matrix method ^[20]^[21]^[22]^[23]^[24] that, given the success of surface treatment and reduction of absorption, shows how many layers have to be applied to reduce transmission accordingly.

The goal is to increase the quality factor of the cavity until Rayleigh scattering of the HeNe gas in the cavity or other unavoidable loss mechanisms set a limit. For simplicity we assume normal incidence. Introducing the complex index of refraction (n_h - jk_h) (where n_h is the real index of refraction and k_h is the extinction coefficient) of the high-index material h [TiO
2]), and a corresponding complex index for the low-index material l [SiO
2], the stack is described by two matrices:

M_r = 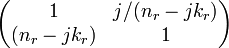$\left( \begin{matrix} 1 & j/(n_{r}-jk_{r}) \\ (n_{r}-jk_{r}) & 1 \\ \end{matrix} \right)$ r = l,h, which are multiplied in pairs, according to the size of the stack: M_h M_l M_hM_l..............M_h M_l. Hereby, all calculations are strictly carried out up to the first power in the k’s, assuming the materials are weakly absorbing. The final result, after the stack is matched to the incoming medium (vacuum) and to the substrate ^[18] (the substrate index is n_s), is:

1 - r = (4n_s/n_h)(n_l/n_h)^2N + 2π(k_h + k_l)/(n_h² - n_l²), where the first term is the Abélès limit,^[21] the second term the Koppelmann limit.^[22] The first term can be made as small as desirable by increasing the stack, N (n_l<n<sub>h). Thus it remains to decrease the extinction coefficients. N is then an adjustable parameter to minimize the overall losses (stacks with up to 50 pairs have been published).

Large rings

The perimeter dependence of the Signal/Noise ratio is ^[25]

$\text{ }S/N\propto L^{3}[1-e^{-(\frac{L_{crit}}{L})^{2}}]^{\frac{1}{2}}$

This equation defines large rings with L >> L_crit ≈ 40 cm, where S/N becomes proportional to L². Therefore the sensitivity of large rings increases quadratically with size, hence the quest for ever larger Ring Lasers for Research.

In the past it was thought that only small ring lasers avoid multimode excitation.^[25] However, if signal bandwidth is sacrificed, there is no known limit to ring laser size, either theoretically or experimentally.^[26]

One of the major advantages of large rings is a quartic reduction of lock-in and pulling in large rings.

Practical rings

Figure 2 shows a practical gas laser gyro of the type that is used in vehicles.

Ring lasers are sometimes modified to allow only one direction of propagation by placing a device into the ring which leads to different losses for different propagation directions. For instance, this could be a Faraday rotator combined with a polarizing element.^[2]

One type of ring laser design is a single crystal design, where light reflects around inside the laser crystal so as to circulate in a ring. This is the "monolithic crystal" design, and such devices are known as "non-planar ring oscillators" (NPROs) or MISERs.^[2] There are also ring fiber lasers.^[3]^[4]

Semiconductor ring lasers have potential applications in all-optical computing. One primary application is as an optical memory device where the direction of propagation represents either 0 or 1. They can maintain the propagation of light in exclusively the clockwise or counterclockwise direction as long as they remain powered.

References

↑ Post, E.J. (1967). "Sagnac effect". Rev. Mod. Phys. 39 (2): 475–493. Bibcode:1967RvMP...39..475P. doi:10.1103/RevModPhys.39.475.
↑ 2.0 2.1 2.2 Paschotta, R (2008). "Ring Lasers". Encyclopedia of Laser Physics and Technology. Wiley. ISBN 978-3-527-40828-3.
↑ 3.0 3.1 Duling III, I.N. (1991). "All-fiber ring soliton laser mode locked with a nonlinear mirror". Opt. Lett. 16 (8): 539–541. Bibcode:1991OptL...16..539D. doi:10.1364/OL.16.000539.
↑ 4.0 4.1 L. E. Nelson et al., “Ultrashort-pulse fiber ring lasers”, Appl. Phys. B 65, 277 (1997)
↑ Rosenthal, A.H. (1962). "Regenerative Circulatory Multiple-Beam Interferometry for the Study of Light-Propagation Effects". J. Opt. Soc. Am. 52 (10): 1143–7. doi:10.1364/JOSA.52.001143.
↑ 6.0 6.1 Macek, W.M.; Davis Jr., D.T.M. (1963). "Rotation rate sensing with traveling-wave ring laser". Appl. Phys. Lett. 2 (3): 67–68. Bibcode:1963ApPhL...2...67M. doi:10.1063/1.1753778.
↑ Sagnac, G. (1914). "Éffet tourbillonnaire optique. La circulation de L'Éther lumineux dans un interférographe tournant". J. de phys. et le radium. 5 4: 177–195.
↑ Stedman, G.E.; Bilger, H.R. (1992). "Ringlaser, an ultrahigh-resolution detector of optical nonreciprocities". Digital Signal Processing 2 (2): 105–9. doi:10.1016/1051-2004(92)90031-S.
↑ Schreiber, K.U.; Velikoseltev, A.; Rothacher, M.; Kluegel, T.; Stedman, G.E.; Wiltshire, D.L. (2004). "Direct measurement of diurnal polar motion by ring laser gyroscopes". J. Geophys. Res. 109 (B6): B06405. arXiv:physics/0406156. Bibcode:2004JGRB..109.6405S. doi:10.1029/2003JB002803.
↑ Sayeh, M.R.; Bilger, H.R. (1985). "Flicker noise in frequency fluctuations of lasers". Phys. Rev. Lett. 55 (7): 700–2. Bibcode:1985PhRvL..55..700S. doi:10.1103/PhysRevLett.55.700.
↑ 11.0 11.1 Statz, H.; Dorschner, T.A.; Holz, M.; Smith, I.W. (1985). "The multioscillator ring laser gyroscope". In Arecchi, F.T.; Stitch, M.L.; Bass, M. et al. Laser Handbook 4. North-Holland. pp. 231–327. ISBN 0444869271. |displayeditors= suggested (help)
↑ Chiao, R.Y.; Moulthrop, A.A.; Levinson, M.T. (1984). "A Josephson gyroscope using superfluids". In Jacobs, S.F.; Physics of Quantum Electronics (Group). Physics of optical ring gyros: 7–10 January 1984, Snowbird, Utah 487. SPIE—the International Society for Optical Engineering. ISBN 978-0-89252-522-5.
↑ 13.0 13.1 Schawlow, A.L.; Townes, C.H. (1958). "Infrared and optical masers". Phys. Rev. 112: 1940–9. Bibcode:1958PhRv..112.1940S. doi:10.1103/PhysRev.112.1940.
↑ 14.0 14.1 14.2 J. T. Verdeyen, “Laser Electronics”, Third Edition, Prentice Hall Series in Solid State Electronics, 1981.
↑ Bilger, H.R.; Stedman, G.E. (1987). "Stability of planar ring lasers with mirror misalignment". Appl. Opt. 26 (17): 3710–6. Bibcode:1987ApOpt..26.3710B. doi:10.1364/AO.26.003710.
↑ Bilger, H.R.; Stedman, G.E.; Wells, P.V. (1990). "Geometrical dependence of polarization in near-planar ring lasers". Opt. Comm. 80: 133–7. Bibcode:1990OptCo..80..133B. doi:10.1016/0030-4018(90)90374-3.
↑ Hoeling, B.; Leuchs, G.; Ruder, H.; Schneider, M. (1992). "An argon ion ring laser as a gyroscope". Appl. Phys. B 55: 46–50. Bibcode:1992ApPhB..55...46H. doi:10.1007/BF00348612.
↑ 18.0 18.1 Bilger, H.R.; Wells, P.V.; Stedman, G.E. (1994). "Origins of fundamental limits for reflection losses at multilayer dielectic mirrors". Appl. Opt. 33 (31): 7390–6. doi:10.1364/AO.33.007390.
↑ 19.0 19.1 Macleod, H.A. (1992). "New techniques revolutionize thin-film optical coatings". Laser Focus World 28 (11): 116–9.
↑ P. Rouard, “Études des propriétés optiques des lames metalliques très minces”, Ann. Phys. (Paris) 7, pp. 291-384 (1937).
↑ 21.0 21.1 F. Abélès, “Investigations on the propagation of sinusoidal electromagnetic waves in stratified media: application to thin films”, Ann. de Physique 5, 596-640 (1950).
↑ 22.0 22.1 G. Koppelmann, “Zur Theorie der Wechselschichten aus schwachabsorbierenden Substanzen und ihre Verwendung als Interferometerspiegel”, Ann. Phys. (Leipzig) 7, pp. 388-396 (1960).
↑ M. Born, Optik (Springer-Verlag, Berlin, 1933).
↑ M. Born and E. Wolf, Principles of Optics, 6th ed. (Pergamon, Oxford, 1981), Chap. 1.
↑ 25.0 25.1 R. R. Simpson and R. Hill, “Ring laser geometry and size”, Roy. Aeron. Soc. London, UK, 25 Feb. 1987.
↑ Bilger, H.R.; Stedman, G.E.; Li, Z.; Schreiber, U.; Schneider, M. (1995). "Ring Lasers for Geodesy". IEEE Trans Instrum Meas 44 (2): 468–470. doi:10.1109/19.377882.