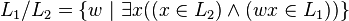Right quotient

The right quotient (or simply quotient) of a formal language 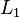$L_1$ with a formal language 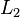$L_2$ is the language consisting of strings w such that wx is in 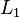$L_1$ for some string x in 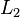$L_2$ .^[1] In symbols, we write:

L_1 / L_2 = \{w \ | \ \exists x ((x \in L_2) \land (wx \in L_1)) \}

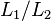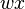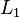In other words, each string in $L_1 / L_2$ is the prefix of a string $wx$ in $L_1$ , with the remainder of the word being a string in $L_2$ .

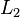Example

Consider

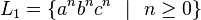
$L_1 = \{ a^n b^n c^n \ \ |\ \ n\ge 0 \}$

and

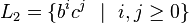$L_2 = \{ b^i c^j \ \ | \ \ i,j\ge 0 \}$ .

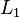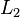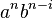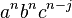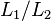Now, if we insert a divider into the middle of an element of $L_1$ , the part on the right is in $L_2$ only if the divider is placed adjacent to a b (in which case i ≤ n and j = n) or adjacent to a c (in which case i = 0 and j ≤ n). The part on the left, therefore, will be either $a^n b^{n-i}$ or $a^n b^n c^{n-j}$ ; and $L_1 / L_2$ can be written as

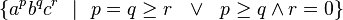\{ a^p b^q c^r \ \ | \ \ p = q \ge r \ \ \or \ \ p \ge q \and r = 0 \}

Properties

Some common closure properties of the right quotient include:

The quotient of a regular language with any other language is regular.
The quotient of a context free language with a regular language is context free.
The quotient of two context free languages can be any recursively enumerable language.
The quotient of two recursively enumerable languages is recursively enumerable.

Left and right quotients

There is a related notion of left quotient, which keeps the postfixes of 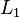$L_1$ without the prefixes in 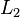$L_2$ . Sometimes, though, "right quotient" is written simply as "quotient". The above closure properties hold for both left and right quotients.

References

↑ Linz, Peter (2011). An Introduction to Formal Languages and Automata. Jones & Bartlett Publishers. pp. 104–108. ISBN 9781449615529. Retrieved 7 July 2014.