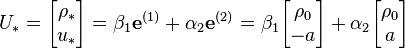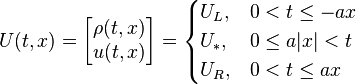Riemann problem
A Riemann problem, named after Bernhard Riemann, consists of an initial value problem composed by a conservation equation together with piecewise constant data having a single discontinuity. The Riemann problem is very useful for the understanding of this kind of equations like Euler conservation equations because all properties, such as shocks and rarefaction waves, appear as characteristics in the solution. It also gives an exact solution to some complex nonlinear equations, such as the Euler equations.
In numerical analysis, Riemann problems appear in a natural way in finite volume methods for the solution of equation of conservation laws due to the discreteness of the grid. For that it is widely used in computational fluid dynamics and in MHD simulations. In these fields Riemann problems are calculated using Riemann solvers.
The Riemann problem in linearized gas dynamics
As a simple example, we investigate the properties of the one dimensional Riemann problem in gas dynamics, which initial condition is defined by
where x = 0 separates two different states, together with the linearised gas dynamic equation (see gas dynamics for derivation).
where we can assume w.o.l.g. 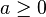 .
We now can rewrite the above equation in conservative form
.
We now can rewrite the above equation in conservative form 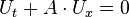 :
:
The eigenvalues of the system are the characteristics of the system
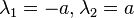 . They give the propagation speed of the medium, including that of any discontinuity, which is the speed of sound here. The corresponding eigenvectors are
. They give the propagation speed of the medium, including that of any discontinuity, which is the speed of sound here. The corresponding eigenvectors are
By decomposing the left state 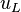 in terms of the eigenvectors, we get for some
in terms of the eigenvectors, we get for some 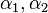
Now we can solve for 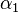 and
and 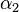 :
:
Analogously
for
Using this, in the domain in between the two characteristics 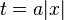 ,
we get the final constant solution
,
we get the final constant solution
and the (piecewise constant) solution in the entire domain 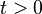 :
:
As this is just a simple example, it still shows the basic properties. Most important the characteristics which decompose the solution into three domains. The propagation speed of these two equations is equivalent to the propagations speed of the sound.
The fastest characteristic defines the Courant–Friedrichs–Lewy (CFL) condition, which sets the restriction for the maximum time step in a computer simulation. Generally as more conservation equations are used, the more characteristics are involved.
References
- Toro, Eleuterio F. (1999). Riemann Solvers and Numerical Methods for Fluid Dynamics. Berlin: Springer Verlag. ISBN 3-540-65966-8.
- LeVeque, Randall J. (2004). Finite-Volume Methods for Hyperbolic Problems. Cambridge: Cambridge University Press. ISBN 0-521-81087-6.
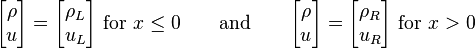
![\begin{align}
\frac{\partial\rho}{\partial t} + \rho_0 \frac{\partial u}{\partial x} & = 0 \\[8pt]
\frac{\partial u}{\partial t} + \frac{a^2}{\rho_0} \frac{\partial \rho}{\partial x} & = 0
\end{align}](../I/m/d77547b1bf98c5adc0629fcb0e80def4.png)
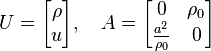

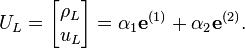
![\begin{align}
\alpha_1 & = \frac{a \rho_L - \rho_0 u_L}{2a\rho_0} \\[8pt]
\alpha_2 & = \frac{a \rho_L + \rho_0 u_L}{2a\rho_0}
\end{align}](../I/m/26a31a698a2c3435e7e1f38e98f04c00.png)
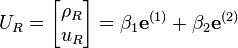
![\begin{align}
\beta_1 & = \frac{a \rho_R - \rho_0 u_R}{2a\rho_0} \\[8pt]
\beta_2 & = \frac{a \rho_R + \rho_0 u_R}{2a\rho_0}
\end{align}](../I/m/0efee79db78256ed4e08e9d107dc2811.png)