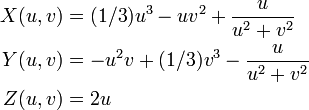Richmond surface

Richmond surface for m=2.

In differential geometry, a Richmond surface is a minimal surface first described by Herbert William Richmond in 1904. [1] It is a family of surfaces with one planar end and one Enneper surface-like self-intersecting end.

It has Weierstrass–Enneper parameterization 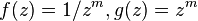f(z)=1/z^m, g(z)=z^m. This allows a parametrization based on a complex parameter as

\begin{align} X(z) &= \Re[(-1/2z) - z^{2m+1}/(4m+2)]\\ Y(z) &= \Re[(-i/2z) + i z^{2m+1}/(4m+2)]\\ Z(z) &= \Re[z^n / n] \end{align}

The associate family of the surface is just the surface rotated around the z-axis.

Taking m = 2 a real parametric expression becomes:[2]

\begin{align} X(u,v) &= (1/3)u^3 - uv^2 + \frac{u}{u^2+v^2}\\ Y(u,v) &= -u^2v + (1/3)v^3 - \frac{u}{u^2+v^2}\\ Z(u,v) &= 2u \end{align}

References

  1. ↑ Jesse Douglas, Tibor Radó, The Problem of Plateau: A Tribute to Jesse Douglas & Tibor Radó, World Scientific, 1992 (p. 239-240)
  2. ↑ John Oprea, The Mathematics of Soap Films: Explorations With Maple, American Mathematical Soc., 2000