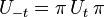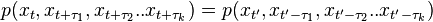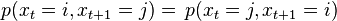Reversible dynamics

For reversibility in thermodynamics, see reversible process (thermodynamics). For further meanings of reversibility, see reversibility (disambiguation).

Mathematics

In mathematics, a dynamical system is invertible if the forward evolution is one-to-one, not many-to-one; so that for every state there exists a well-defined reverse-time evolution operator.

The dynamics are time-reversible if there exists a transformation (an involution) π which gives a one-to-one mapping between the time-reversed evolution of any one state, and the forward-time evolution of another corresponding state, given by the operator equation:

U_{-t} = \pi \, U_{t}\, \pi

Any time-independent structures (for example critical points, or attractors) which the dynamics gives rise to must therefore either be self-symmetrical or have symmetrical images under the involution π.

Physics

In physics, the laws of motion of classical mechanics have the above property, if the operator π reverses the conjugate momenta of all the particles of the system, p -> -p . (T-symmetry).

In quantum mechanical systems, it turns out that the weak nuclear force is not invariant under T-symmetry alone. If weak interactions are present, reversible dynamics are still possible, but only if the operator π also reverses the signs of all the charges, and the parity of the spatial co-ordinates (C-symmetry and P-symmetry).

Thermodynamic systems might be reversible or irreversible.

Stochastic processes

A stochastic process is reversible if the statistical properties of the process are the same as the statistical properties for time-reversed data from the same process. More formally, for all sets of time increments { τs }, where s = 1..k for any k, the joint probabilities

p(x_t, x_{t+\tau_{1}}, x_{t+\tau_{2}} .. x_{t+\tau_{k}}) = p(x_{t'}, x_{t'-\tau_{1}}, x_{t'-\tau_{2}} .. x_{t'-\tau_{k}})

A simple consequence for Markov processes is that they can only be reversible if their stationary distributions have the property

p(x_t=i,x_{t+1}=j) = \,p(x_t=j,x_{t+1}=i)

This is called the property of detailed balance.

See also