Restriction of scalars
In abstract algebra, restriction of scalars is a procedure of creating a module over a ring 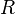 from a module over another ring
from a module over another ring  , given a homomorphism
, given a homomorphism 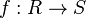 between them. Intuitively speaking, the resulting module "remembers" less information than the initial one, hence the name.
between them. Intuitively speaking, the resulting module "remembers" less information than the initial one, hence the name.
In algebraic geometry, the term "restriction of scalars" is often used as a synonym for Weil restriction.
Definition
Let 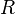 and
and  be two rings (they may or may not be commutative, or contain an identity), and let
be two rings (they may or may not be commutative, or contain an identity), and let 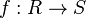 be a homomorphism. Suppose that
be a homomorphism. Suppose that 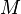 is a module over
is a module over  . Then it can be regarded as a module over
. Then it can be regarded as a module over 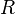 , if the action of
, if the action of 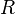 is given via
is given via 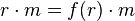 for
for 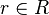 and
and 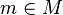 .
.
Interpretation as a functor
Restriction of scalars can be viewed as a functor from  -modules to
-modules to 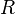 -modules. An
-modules. An  -homomorphism
-homomorphism 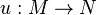 automatically becomes an
automatically becomes an 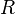 -homomorphism between the restrictions of
-homomorphism between the restrictions of 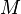 and
and 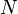 . Indeed, if
. Indeed, if 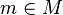 and
and 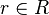 , then
, then
-
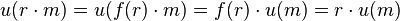 .
.
As a functor, restriction of scalars is the right adjoint of the extension of scalars functor.
If 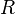 is the ring of integers, then this is just the forgetful functor from modules to abelian groups.
is the ring of integers, then this is just the forgetful functor from modules to abelian groups.
The case of fields
When both 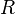 and
and  are fields,
are fields, 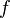 is necessarily a monomorphism, and so identifies
is necessarily a monomorphism, and so identifies 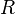 with a subfield of
with a subfield of  . In such a case an
. In such a case an  -module is simply a vector space over
-module is simply a vector space over  , and naturally over any subfield thereof. The module obtained by restriction is then simply a vector space over the subfield
, and naturally over any subfield thereof. The module obtained by restriction is then simply a vector space over the subfield 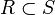 .
.