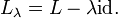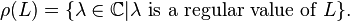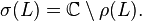Resolvent set
In linear algebra and operator theory, the resolvent set of a linear operator is a set of complex numbers for which the operator is in some sense "well-behaved". The resolvent set plays an important role in the resolvent formalism.
Definitions
Let X be a Banach space and let 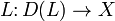 be a linear operator with domain
be a linear operator with domain 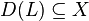 . Let id denote the identity operator on X. For any
. Let id denote the identity operator on X. For any 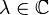 , let
, let
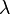 is said to be a regular value if
is said to be a regular value if 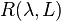 , the inverse operator to
, the inverse operator to 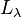
- exists;
- is a bounded linear operator;
- is defined on a dense subspace of X.
The resolvent set of L is the set of all regular values of L:
The spectrum is the complement of the resolvent set:
The spectrum can be further decomposed into the point/discrete spectrum (where condition 1 fails), the continuous spectrum (where conditions 1 and 3 hold but condition 2 fails) and the residual/compression spectrum (where condition 1 holds but condition 3 fails).
Properties
- The resolvent set
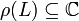 of a bounded linear operator L is an open set.
of a bounded linear operator L is an open set.
References
- Renardy, Michael; Rogers, Robert C. (2004). An introduction to partial differential equations. Texts in Applied Mathematics 13 (Second ed.). New York: Springer-Verlag. xiv+434. ISBN 0-387-00444-0. MR 2028503 (See section 8.3)
External links
- Voitsekhovskii, M.I. (2001), "Resolvent set", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4