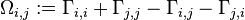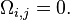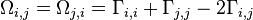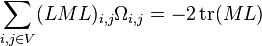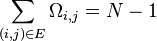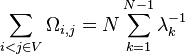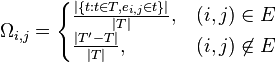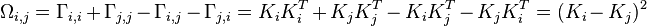Resistance distance
In graph theory, the resistance distance between two vertices of a simple connected graph, G, is equal to the resistance between two equivalent points on an electrical network, constructed so as to correspond to G, with each edge being replaced by a 1 ohm resistance. It is a metric on graphs.
Definition
On a graph G, the resistance distance Ωi,j between two vertices vi and vj is
where Γ is the Moore–Penrose inverse of the Laplacian matrix of G.
Properties of resistance distance
If i = j then
For an undirected graph
General sum rule
For any N-vertex simple connected graph G = (V, E) and arbitrary N×N matrix M:
From this generalized sum rule a number of relationships can be derived depending on the choice of M. Two of note are;
where the 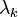 are the non-zero eigenvalues of the Laplacian matrix. This unordered sum Σi<jΩi,j is called the Kirchhoff index of the graph.
are the non-zero eigenvalues of the Laplacian matrix. This unordered sum Σi<jΩi,j is called the Kirchhoff index of the graph.
Relationship to the number of spanning trees of a graph
For a simple connected graph G = (V, E), the resistance distance between two vertices may by expressed as a function of the set of spanning trees, T, of G as follows:
where 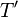 is the set of spanning trees for the graph
is the set of spanning trees for the graph 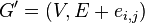 .
.
As a squared Euclidean distance
Since the Laplacian  is symmetric and positive semi-definite, its pseudoinverse
is symmetric and positive semi-definite, its pseudoinverse 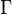 is also symmetric and positive semi-definite. Thus, there is a
is also symmetric and positive semi-definite. Thus, there is a  such that
such that 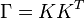 and we can write:
and we can write:
showing that the square root of the resistance distance corresponds to the Euclidean distance in the space spanned by  .
.
Connection with Fibonacci numbers
A fan graph is a graph on 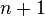 vertices where there is an edge between vertex
vertices where there is an edge between vertex  and
and 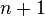 for all
for all 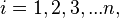 and there is an edge between vertex
and there is an edge between vertex  and
and 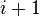 for all
for all 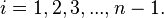
The resistance distance between vertex 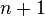 and vertex
and vertex 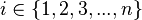 is
is 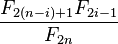 where
where 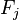 is the
is the 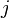 -th Fibonacci number, for
-th Fibonacci number, for 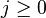 .[1][2]
.[1][2]
See also
References
- Klein, D. J.; Randic, M. J. (1993). "Resistance Distance". J. Math. Chem. 12: 81. doi:10.1007/BF01164627.
- Gutman, Ivan; Mohar, Bojan (1996). "The quasi-Wiener and the Kirchhoff indices coincide". J. Chem. Inf. Comput. Sci. 36: 982–985. doi:10.1021/ci960007t.
- Palacios, Jose Luis (2001). "Closed-form formulas for the Kirchhoff index". Int. J. Quant. Chem. 81: 135–140. doi:10.1002/1097-461X(2001)81:2<135::AID-QUA4>3.0.CO;2-G.
- Babic, D.; Klein, D. J.; Lukovits, I.; Nikolic, S.; Trinajstic, N. (2002). "Resistance-distance matrix: a computational algorithm and its application". Int. J. Quant. Chem. 90 (1): 166–167. doi:10.1002/qua.10057.
- Klein, D. J. (2002). "Resistance Distance Sum Rules" (PDF). Croatica Chem. Acta 75 (2): 633–649.
- Bapat, Ravindra B.; Gutman, Ivan; Xiao, Wenjun (2003). "A simple method for computing resistance distance". Z. Naturforsch. 58a: 494–498.
- Placios, Jose Luis (2004). "Foster's formulas via probability and the Kirchhoff index". Method. Comput. Appl. Probab. 6 (4): 381–387. doi:10.1023/B:MCAP.0000045086.76839.54.
- Bendito, Enrique; Carmona, Angeles; Encinas, Andres M.; Gesto, Jose M. (2008). "A formula for the Kirhhoff index". Int. J. Quant. Chem. 108 (6): 1200–1206. Bibcode:2008IJQC..108.1200B. doi:10.1002/qua.21588.
- Zhou, Bo; Trinajstic, Nenad (2009). "The Kirchhoff index and the matching number". Int. J. Quant. Chem. 109: 2978–2981. Bibcode:2009IJQC..109.2978Z. doi:10.1002/qua.21915.
- Zhou, Bo; Trinajstic, Nenad (2009). "On resistance-distance and the Kirchhoff index". J. Math. Chem. 46: 283–289. doi:10.1007/s10910-008-9459-3.
- Zhou, Bo. "On sum of powers of Laplacian eigenvalues and Laplacian Estrada Index of graphs". arXiv:1102.1144.
- Zhang, Heping; Yang, Yujun (2007). "Resistance distance and Kirchhoff index in circulant graphs". Int. J. Quantum Chem. 107: 330–339. Bibcode:2007IJQC..107..330Z. doi:10.1002/qua.21068.
- Yang, Yujun; Zhang, Heping (2008). "Some rules on resistance distance with applications". J. Phys. A: Math. Theor. 41: 445203. Bibcode:2008JPhA...41R5203Y. doi:10.1088/1751-8113/41/44/445203.