Reshetnyak gluing theorem

In metric geometry, the Reshetnyak gluing theorem gives information on the structure of a geometric object build by using as building blocks other geometric objects, belonging to a well defined class. Intuitively, it states that a manifold obtained by joining (i.e. "gluing") together, in a precisely defined way, other manifolds having a given property inherit that very same property.

The theorem was first stated and proved by Yurii Reshetnyak in 1968.^[1]

Statement

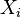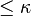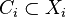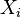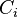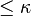Theorem: Let $X_i$ be complete locally compact geodesic metric spaces of CAT curvature $\leq \kappa$ , and $C_i\subset X_i$ convex subsets which are isometric. Then the manifold $X$ , obtained by gluing all $X_i$ along all $C_i$ , is also of CAT curvature $\leq \kappa$ .

For an exposition and a proof of the Reshetnyak Gluing Theorem, see (Burago, Burago & Ivanov 2001, Theorem 9.1.21).

Notes

↑ See the original paper by Reshetnyak (1968) or the book by Burago, Burago & Ivanov (2001, Theorem 9.1.21).

References

Reshetnyak, Yu. G. (1968), "Nonexpanding maps in spaces of curvature not greater than $K$ ", Sibirskii Matematicheskii Zhurnal (in Russian) 9 (4): 918–927, MR 0244922, Zbl 0167.50803 , translated in English as:
- "Inextensible mappings in a space of curvature no greater than $K$ ", Siberian Mathematical Journal 9 (4), 1968: 683–689, doi:10.1007/BF02199105, Zbl 0176.19503 .
Burago, Dmitri; Burago, Yuri; Ivanov, Sergei (2001), A course in metric geometry, Graduate Studies in Mathematics 33, Providence, RI: American Mathematical Society, pp. xiv+415, ISBN 0-8218-2129-6, MR 1835418, Zbl 0981.51016 .