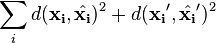Reprojection error

The reprojection error is a geometric error corresponding to the image distance between a projected point and a measured one. It is used to quantify how closely an estimate of a 3D point 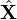$\hat{\mathbf{X}}$ recreates the point's true projection 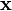$\mathbf{x}$ . More precisely, let 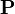$\mathbf{P}$ be the projection matrix of a camera and 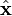$\hat{\mathbf{x}}$ be the image projection of 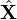$\hat{\mathbf{X}}$ , i.e. 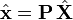$\hat{\mathbf{x}}=\mathbf{P} \, \hat{\mathbf{X}}$ . 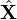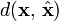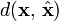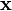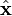The reprojection error of $\hat{\mathbf{X}}$ is given by $d(\mathbf{x}, \, \hat{\mathbf{x}})$ , where $d(\mathbf{x}, \, \hat{\mathbf{x}})$ denotes the Euclidean distance between the image points represented by vectors $\mathbf{x}$ and $\hat{\mathbf{x}}$ .

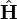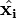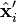Minimizing the reprojection error can be used for estimating the error from point correspondences between two images. Suppose we are given 2D to 2D point imperfect correspondences $\{\mathbf{x_i} \leftrightarrow \mathbf{x_i}'\}$ . We wish to find a homography $\hat{\mathbf{H}}$ and pairs of perfectly matched points $\hat{\mathbf{x_i}}$ and $\hat{\mathbf{x}}_i'$ , i.e. points that satisfy 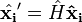$\hat{\mathbf{x_i}}' = \hat{H}\mathbf{\hat{x}_i}$ that minimize the reprojection error function given by

\sum_i d(\mathbf{x_i}, \hat{\mathbf{x_i}})^2 + d(\mathbf{x_i}', \hat{\mathbf{x_i}}')^2

So the correspondences can be interpreted as imperfect images of a world point and the reprojection error quantifies their deviation from the true image projections 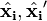$\hat{\mathbf{x_i}}, \hat{\mathbf{x_i}}'$

References

Richard Hartley and Andrew Zisserman (2003). Multiple View Geometry in computer vision. Cambridge University Press. ISBN 0-521-54051-8.