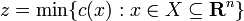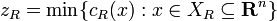Relaxation (approximation)

In mathematical optimization and related fields, relaxation is a modeling strategy. A relaxation is an approximation of a difficult problem by a nearby problem that is easier to solve. A solution of the relaxed problem provides information about the original problem.

For example, a linear programming relaxation of an integer programming problem removes the integrality constraint and so allows non-integer rational solutions. A Lagrangian relaxation of a complicated problem in combinatorial optimization penalizes violations of some constraints, allowing an easier relaxed problem to be solved. Relaxation techniques complement or supplement branch and bound algorithms of combinatorial optimization; linear programming and Lagrangian relaxations are used to obtain bounds in branch-and-bound algorithms for integer programming.[1]

The modeling strategy of relaxation should not be confused with iterative methods of relaxation, such as successive over-relaxation (SOR); iterative methods of relaxation are used in solving problems in differential equations, linear least-squares, and linear programming.[2][3][4] However, iterative methods of relaxation have been used to solve Lagrangian relaxations.[5]

Definition

A relaxation of the minimization problem

z = \min \{c(x) : x \in X \subseteq \mathbf{R}^{n}\}

is another minimization problem of the form

z_R = \min \{c_R(x) : x \in X_R \subseteq \mathbf{R}^{n}\}

with these two properties

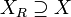
  1. X_R \supseteq X
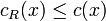  2. c_R(x) \leq c(x) for all x \in X.

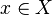The first property states that the original problem's feasible domain is a subset of the relaxed problem's feasible domain. The second property states that the original problem's objective-function is greater than or equal to the relaxed problem's objective-function.[1]

Properties

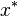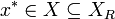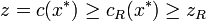If x^* is an optimal solution of the original problem, then x^* \in X \subseteq X_R and z = c(x^*) \geq c_R(x^*)\geq z_R. Therefore 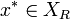x^* \in X_R provides an upper bound on z_R.

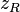If in addition to the previous assumptions, 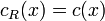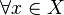c_R(x)=c(x), \forall x\in X, the following holds: If an optimal solution for the relaxed problem is feasible for the original problem, then it is optimal for the original problem.[1]

Some relaxation techniques

Notes

  1. ↑ 1.0 1.1 1.2 Geoffrion (1971)
  2. ↑ Murty, Katta G. (1983). "16 Iterative methods for linear inequalities and linear programs (especially 16.2 Relaxation methods, and 16.4 Sparsity-preserving iterative SOR algorithms for linear programming)". Linear programming. New York: John Wiley & Sons, Inc. pp. 453–464. ISBN 0-471-09725-X. MR 720547.
  3. ↑ Goffin, J.-L. (1980). "The relaxation method for solving systems of linear inequalities". Math. Oper. Res. 5 (3): 388–414. doi:10.1287/moor.5.3.388. JSTOR 3689446. MR 594854.
  4. ↑ Minoux, M. (1986). Mathematical programming: Theory and algorithms. Egon Balas (foreword) (Translated by Steven Vajda from the (1983 Paris: Dunod) French ed.). Chichester: A Wiley-Interscience Publication. John Wiley & Sons, Ltd. pp. xxviii+489. ISBN 0-471-90170-9. MR 868279. (2008 Second ed., in French: Programmation mathématique: Théorie et algorithmes. Editions Tec & Doc, Paris, 2008. xxx+711 pp. ISBN 978-2-7430-1000-3.. MR 2571910)
  5. ↑ Relaxation methods for finding feasible solutions to linear inequality systems arise in linear programming and in Lagrangian relaxation. Goffin (1980) and Minoux (1986)|loc=Section 4.3.7, pp. 120–123 cite Shmuel Agmon (1954), and Theodore Motzkin and Isaac Schoenberg (1954), and L. T. Gubin, Boris T. Polyak, and E. V. Raik (1969).

References