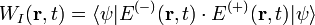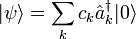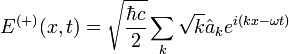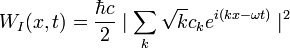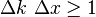Relational approach to quantum physics
- This article is intended for those already familiar with quantum mechanics and its attendant interpretational difficulties. Readers who are new to the subject may first want to read the introduction to quantum mechanics.
The relational approach to quantum physics is an alternative approach to and interpretation of quantum mechanics. It asserts that the physical world can only be studied accurately in terms of relationships between systems, as all experimentally verifiable facts about the world result explicitly from interactions (such as the interaction between a light field and a detector). According to the relational approach, the assumption that objects possess absolute properties (such as an absolute particle, independent of any detection frame) inevitably leads to ambiguities and paradoxes when these objects are studied closely. The approach was adopted, in a time span of 1992-1996, by Q. Zheng, S. Hughes, and T. Kobayashi in the University of Tokyo.[1] As early as in 1985, S. Kochen suggested that the paradoxes of quantum physics could be overcome by developing a relational approach, which was needed at one time to solve the paradoxes of relativistic physics of space and time.[2][3] It is also hoped that this entry will serve as a complement to Rovelli’s relational quantum mechanics (RQM).
Historically, the theory of relativity and quantum mechanics were intertwined with each other and the compatibility between both theories was a main theme throughout the Bohr-Einstein debate.[4] In both theories the physicists emphasized that only measurable quantities, that is, observables, belong in a theory. Bohr compared his approach to Einstein’s theory of relativity and asserted that in the treatment of quantum processes the complementarity of the measuring results cannot be ignored, just as in high-speed phenomena the relativity of observation cannot be neglected when the simultaneity comes into question. But Einstein replied: “A good joke should not be repeated too often.” [5] The debate continued in connection with Einstein-Podolsky-Rosen (EPR) paradox, and Bohr proposed the relational conception of quantum states.[6] Through their analysis Bohm and Schumacher concluded that the characteristic feature of this debate is the failure to communicate due to the absence of a full harmony of quantum mechanics with relativity.[7]
Modern attempts to embrace a relational approach with interpretations of quantum mechanics have been tried many times, ranging from Everett's relative-state interpretation (Everett, 1957), sigma algebra of interactive properties (Kochen, 1979), quantum reference systems (Bene, 1992), quantum theory of the universe (Smolin, 1995), to relational quantum mechanics (Rovelli, 1996). They more or less emphasize the relational nature of quantum states. For more information, please refer to the further reading list.
Background
As is well known, Einstein's theory of relativity, which involves a profound analysis of time and space, introduced radical changes, not only in our basic concepts, but also in our modes of physical reasoning. The essence of Einstein's theory was to adopt a relational approach to the notions of time and space,[8] which mathematically can be expressed through the Lorentz space-time transformations.
Although the mathematical structure of the Lorentz ether theory, which leaves the speed of light in vacuo, c, a universal constant, is equivalent to that of Einstein's, there is nevertheless a drastic difference in the way to conceive it. On the one hand, Lorentz began with retaining the customary concepts of absolute time and space of the older Newtonian mechanics, and by considering changes in the observing instruments. The invariant nature of c, as measured experimentally from the Michelson-Morley experiment, was successfully explained by the so-called 'Lorentz contraction', moving through the hypothetical ether. However, this theory led to the difficulty that the exact values of the 'true' distances and times, with respect to a detection scheme at rest in the ether, became somewhat ambiguous and unknowable. Einstein, on the other hand, by commencing with the observed facts, regarded time and space a priori as a certain class of 'coordinates' merely expressing relationships of an event to the measuring instruments. On the basis of a constant speed of light, both time and space become relative concepts, fundamentally dependent of the observer.
The developments of quantum formulation early this century has also led physicists to question the Newtonian concepts of physical objects, such as 'particle' and 'wave', which are basic ideas in all of classical physics. Subsequently, Heisenberg in his pioneering paper [9] developed a conceptual framework that in a way retained all the classical concepts, and plays a great role in the Copenhagen interpretation. This basic new step was to study the disturbance of observing instruments, and for this purpose, Heisenberg constructed the famous gedanken microscope experiment to measure very accurately the position of an electron. It was found that since the individual quanta of action must be taken into account in the measurement process, the irreducible disturbance rendered it impossible to assign simultaneously the precise values of position and momentum. Consequently, by considering the uncontrollable influence from the observation itself, the notion of particle into quantum mechanics was preserved, and the uncertainty principle was born.
Inherent ambiguity in Heisenberg’s uncertainty principle
In spite of its successes however, the Heisenberg theory has also brought about the problem, in a similar manner to the Lorentz theory,[10] that the fundamental concepts, e.g., the notion of particle in the interpretation, are in fact completely ambiguous. For it is deduced on the basis of the Heisenberg uncertainty principle that no means could ever give precisely a 'true' particle simultaneous values of position and momentum. This has been the object of severe criticisms from some other famous physicists, like Einstein, who has always believed that even in quantum theory there must exist precisely definable elements or dynamical variables to determine the actual behavior of each individual system.[11] In view of this fundamental ambiguity, it seems evident that a careful analysis of the notion of particle based on the actually measured facts is required, in parallel to Einstein's analysis of time.
In a paper published in 1996,[12] Zheng et al. developed a relational approach to wave-particle duality which avoids the ambiguity associated with the Heisenberg theory. They emphasize, in parallel with Einstein's theory of special relativity, that for the proper analysis of quantum optics measurements with different frames of detection, one must consult a conceptual map of events which takes into account the perspective of the observer implicitly. The importance of events in quantum theory has been emphasized recently,[13] which for quantum optics can be described mathematically in terms of light detection, pioneered by Roy J. Glauber.[14]
The presence of a physical object can be established by interaction in which detection events serve as relationships between the object and the class of the measuring instrument. In other words, all our actual knowledge of a physical object is based on, at least in principle, the experimentally detected relationships between the object and a suitable detector.
In the quantum theory of radiation, the electric field operator in the Coulomb gauge may be written as the sum of positive and negative frequency parts, Eq. (1):
where
One may expand 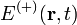 in terms of the normal modes as follows:
in terms of the normal modes as follows:
where 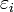 are the unit vectors of polarization; this expansion has the same form as the classical expansion except that now the field amplitudes
are the unit vectors of polarization; this expansion has the same form as the classical expansion except that now the field amplitudes 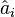 are operators.
are operators.
Glauber has studied the way in which light is detected, and showed that, for an ideal photodetector situated at a point 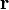 in a radiation field, the probability of observing a photoionization event in this detector between time
in a radiation field, the probability of observing a photoionization event in this detector between time 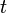 and
and 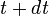 is proportional to
is proportional to 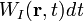 , where, Eq. (2):
, where, Eq. (2):
and 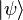 specifies the state of the field. If one considers the one-dimensional propagation problem of one-photon states, constructed by Glauber.[15]
specifies the state of the field. If one considers the one-dimensional propagation problem of one-photon states, constructed by Glauber.[15]
and
Subsequently, the detection probability propagating along the 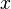 direction becomes:
direction becomes:
This probability of observing photoionization in detectors also reproduces the probabilistic wave of quantum phenomena. The Glauber detection theory differs from the Born probabilistic interpretation,[16] in that it expresses the meaning of physical law in terms of relationships, counting signals in the detection processes, without assuming the particle model of matter. These concepts quite naturally lead to a relational approach for the notion of physical object, and one can say that, in terms of actually measurable counting signals, the detection events follow laws of probability.
Here, one does not regard the above result as a deduction from the Heisenberg theory, but as a basic hypothesis which is well established experimentally. This needs little explanation, e.g., in terms of the disturbance of instruments, but is merely our starting point for further analysis; as in Einstein's theory of special relativity, we start from the fact that the speed of light is a constant.
Analysis of the concept of localizability
One can continue to consider an object's position measurement, in order to see more clearly what this hypothesis implies with regard to the notion of localizability in physics, similar to the discussion of simultaneity in Einstein's theory of special relativity.[17]
In Newtonian mechanics, one can measure an object's position with the aid of a detector. The outcome of a detection event (resulting from the interaction between a detector and the object), or the occurrence of a detection event at a point in space, indicates the position of the object. But as far as Newtonian mechanics is concerned, it is assumed that there is only one position corresponding to an object. This implies that given any detection event at a position (as registered by an accurate detector), similar procedures will produce other detection outcomes in which the measurements will all be co-located at the same point in space as the first event. As a result, no detector carrying out proper position measurements on the object will ever produce results that are different from each other. If this is the case, then it makes sense to ascribe a definite (or "absolute") position to the object, and to say that the object is localized at a point in space.
This is not what is found in quantum theory, however. For instance, the detection of light is described by the measurement of one-photon states. From a general property of Fourier transforms, the wave packet at a given time 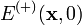 , with a spectrum width
, with a spectrum width 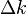 , indicates that the detection of an event can no longer be localized to a specific point in space — i.e., a definite position for the photon — but instead covers a range specified by
, indicates that the detection of an event can no longer be localized to a specific point in space — i.e., a definite position for the photon — but instead covers a range specified by 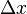 , where
, where
This is a major break with older ideas, because different detection events do not agree on the position of a photon. It must be emphasized, however, that whether localizability can be established is based only on an indirect deduction, the result of a statistical analysis, which expresses the deviation for the detection. Localizability is therefore not an immediate fact by which an object can be described simply as a point mass condensed at a spot in space. Instead, it is seen to depend largely on a purely conventional means of taking into account the deviation of the detected signals. This convention seems natural to our common sense, but it leads to unambiguous results — a definite position for a physical object — only in cases where Newtonian mechanics is a good approximation. When the characteristic widths of 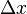 and
and 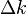 can no longer be regarded as effectively infinite, then the results of empirical experiment make it clear that the measurements depend on the characteristic deviations for the problem in question.
can no longer be regarded as effectively infinite, then the results of empirical experiment make it clear that the measurements depend on the characteristic deviations for the problem in question.
It follows from the above discussion that localizability is not an absolute quality of objects; rather, its significance is dependent upon objects' characteristic deviations, for example the widths of 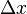 and
and 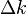 .
.
Consequently, although the mathematical structure of the above approach is equivalent to that of the Heisenberg theory (which leads to the uncertainty principle), the underlying conceptual framework is vastly different. In the Heisenberg theory, one deduces the uncertainty relation as a consequence of the disturbance of observing instruments, as they irreducibly participate in the observation process; subsequently, this infers that a causal description is impossible for quantum theory, and 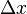 is therefore interpreted as the uncertainty of position. On the contrary, by adopting a relational approach, one begins with the experimentally well-confirmed hypothesis of the probability of detection events, as actually observed. With this starting point, the above inequality implies that the concept of absolute position is no longer meaningful in quantum theory, where
is therefore interpreted as the uncertainty of position. On the contrary, by adopting a relational approach, one begins with the experimentally well-confirmed hypothesis of the probability of detection events, as actually observed. With this starting point, the above inequality implies that the concept of absolute position is no longer meaningful in quantum theory, where 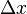 specifies the deviation of detection. Indeed, once it is clear that the absolute position underlying localizability is not valid in quantum mechanics, it immediately follows that new concepts are needed to describe quantum processes, which contain the particle as a limiting case.[18]
specifies the deviation of detection. Indeed, once it is clear that the absolute position underlying localizability is not valid in quantum mechanics, it immediately follows that new concepts are needed to describe quantum processes, which contain the particle as a limiting case.[18]
Analysis of particle and wave concepts in terms of frames of detection
From the above discussion, it is shown that an outcome of detection (an event) specifies only a relationship between that object and a certain detection; however it is not sufficient to consider only the result of an individual detection. The real significance of our detections arises from the fact that the properties of physical objects can be regularized and ordered in terms of frames of detection. For example, in a particle detection frame of light, one arranges a series of photodetectors in the propagation direction, by which one can define invariant quantities such as the velocity of the light signal propagation c (emission and absorption). This allows one not only to establish a 'trajectory' but also relate it to a portion of energy, E, and momentum, p, (a photon), transferred from a light field to a detector, to form a particle picture (p = E/c).
There also exists a wave frame of detection, where, for example, light is divided into two paths so as to interfere with each other. To measure and analyze such an effect, one also needs to place an array of detectors on the interfering plane, from which one can infer an additional set of quantities such as the frequency, wavelength, and also the phase velocity from the interference fringes; thus one constructs a wave picture. However, as far as Newtonian mechanics is concerned, such a wave frame of detection seems to be not necessary, and with the localizability discussed above, it makes sense to ascribe only the concept of particle to the cases investigated in the Newtonian domain.
Of course, all this experience depends on the condition that the de Broglie wavelength is so small that on the ordinary scale of distance and time, the wave modulation in the detection can be neglected; this is equivalent to assuming an infinitely small wavelength of matter. When a finite de Broglie wavelength is taken into account, new problems of 'wave-particle duality' do in fact arise, which ran through the famous Bohr-Einstein debate and is still a key issue in recent discussions.[19]
In terms of detection frames, the implications of the relational approach implies that there is, in fact, no absolute significance to particle and wave pictures, but rather, their meaning is fundamentally dependent on how a frame of detection is constructed, i.e., on the observer. However, this concept of 'relativity', can only be expressed in precise quantitative form by Glauber's theory of light detection that logically unifies the two pictures of particle and wave.
From the relational viewpoint, physical phenomena in the quantum theory of light detection are described in terms of fields 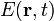 [Eq. (1)] and their detection
[Eq. (1)] and their detection 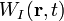 [Eq. (2)], which are organized, ordered, and structured so as to correspond to the characteristics of radiation systems that are being studied. In the aforementioned theory, de Broglie's concepts are now manifested by
[Eq. (2)], which are organized, ordered, and structured so as to correspond to the characteristics of radiation systems that are being studied. In the aforementioned theory, de Broglie's concepts are now manifested by 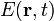 , in terms of annihilation operator
, in terms of annihilation operator 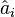 (and creation operator
(and creation operator 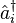 ) as field amplitudes modulated by phase factors
) as field amplitudes modulated by phase factors 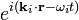 (and the conjugated
(and the conjugated 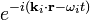 ). The key point that we wish to establish is that
). The key point that we wish to establish is that 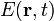 , contains information concerning the propagation properties of light in both the particle and wave frames of detection since on the one hand, the propagation characteristics of the operators
, contains information concerning the propagation properties of light in both the particle and wave frames of detection since on the one hand, the propagation characteristics of the operators 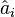 and
and 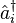 , which physically describe the absorption and emission of light, indicate a particle frame of detection where the light signal travels at the speed c. On the other hand, the phase factor
, which physically describe the absorption and emission of light, indicate a particle frame of detection where the light signal travels at the speed c. On the other hand, the phase factor 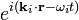 , implies a wave frame of detection, regulated by interference effects in the detection.
It seems clear then that in the quantum theory of light detection, the particle and wave pictures are united as two sets of relative features of the same field in different frames of detection; thus they can be related to each other in such a way that Eq. (1) is left invariant - the principle of relativity. This unification can be characterized by a term called particle-wave rather than 'particle or/and wave', the hyphen emphasizing the new kind of unification.
, implies a wave frame of detection, regulated by interference effects in the detection.
It seems clear then that in the quantum theory of light detection, the particle and wave pictures are united as two sets of relative features of the same field in different frames of detection; thus they can be related to each other in such a way that Eq. (1) is left invariant - the principle of relativity. This unification can be characterized by a term called particle-wave rather than 'particle or/and wave', the hyphen emphasizing the new kind of unification.
It should be noted that in spite of the above-described unification of particle and wave pictures brought about in the quantum theory of detection, there remains a rather important and peculiar distinction between them, resulting from the fact that 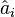 and
and 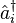 are operators but the phase factors
are operators but the phase factors 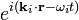 (
(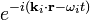 ) are c-numbers. On the basis of this distinction, it also clear that the modulation by the phase factors in the probability expression of Eq. (2) at a velocity (the phase velocity) greater than c, for example, in de Broglie matter systems, in no way confuses us on the maximum speed of propagation of the signals, provided that a signal propagation is physically described by the annihilation and creation operators
) are c-numbers. On the basis of this distinction, it also clear that the modulation by the phase factors in the probability expression of Eq. (2) at a velocity (the phase velocity) greater than c, for example, in de Broglie matter systems, in no way confuses us on the maximum speed of propagation of the signals, provided that a signal propagation is physically described by the annihilation and creation operators 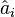 and
and 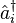 .
.
Mathematical structure of quantum theory as a conceptual map
One can conclude that the Newtonian analysis of the world into constituent objects has been replaced in terms of a kind of interactive pattern between the fields and their detection by the observer. The implications of this approach avoids much of our confusion about the wave-particle duality, if we regard the quantum theory of light detection as a kind of conceptual map of the events in the world, in a similar manner to the Minkowski diagram in Einstein's theory of special relativity.[20]
Because of the relativistic unification of the particle and wave pictures into the single expression of Eq. (1), there appears an illusion of co-existence of these two pictures. However, a little reflection shows that this view of the quantum theory of light detection is very far from the truth indeed. Let us say, for example, that an observer wants to measure the speed of a light signal. He or she must then construct a particle frame of detection that registers where, and when, a light signal is emitted and then absorbed. (We note that the propagation of a light signal is, in fact, what Einstein studied in the development of his special relativity theory). Such an observer cannot survey the whole of Eq. (1); he or she can only obtain the propagation details of the operators 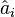 and
and 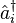 . Therefore, the exact information of the phase factor
. Therefore, the exact information of the phase factor 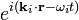 (
(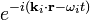 ) is unknown to the observer; for this, an interference experiment is required.
) is unknown to the observer; for this, an interference experiment is required.
Thus, the quantum theory of light detection can be envisioned as a conceptual map, having an invariant structure, containing the 'real' set of fields and their detection which can be observed experimentally. "In all maps (conceptual or otherwise) there arises the need for the user to locate and orient himself by seeing which point on the map represents his position and which line represents the direction in which he is looking".[21] In doing this, one recognizes that every act of actualization yields a unique perspective on the world. But with the aid of the quantum theory of light detection, one can relate what is seen from one perspective (the particle frame) to what is seen from another (the wave frame). In this way one can abstract out what is invariant under a change of perspective, which leads to an ever-improving knowledge and understanding of the actual character of the radiation system under investigation. Therefore, when an observer, performing experiments with different frames of detection, tries to understand what is observed, he or she need not puzzle about which view is 'correct' and which view is 'wrong' (wave or particle). Rather, he or she consults the map provided by Eq. (1) and tries to come to a common understanding of why in each way detecting the same field has a different perspective. Different frames may be related to one another, for example, by employing the de Broglie relation, 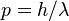 .
.
Notes
- ↑ Zheng et al. (1992, 1996)
- ↑ S. Kochen, Symposium of the Foundations of Modern Physics: 50 Years of the Einstein-Podolsky-Rosen Gedankenexperiment, (World Scientific Publishing Co., Singapore, 1985), pp. 151-69.
- ↑ For later work, see John Conway and Simon Kochen The Free Will Theorem.
- ↑ M. Jammer, The Philosophy of Quantum Mechanics, (Wiley, New York, 1974), p. 109.
- ↑ P. Frank, Einstein-His Life and Times, (Knopf, New York, 1947), p. 216.
- ↑ M. Jammer, The Philosophy of Quantum Mechanics, (Wiley, New York, 1974), p. 197.
- ↑ D. Bohm and D. L. Schumacher, On the failure of communication between Bohr and Einstein, (Preprint, 1972).
- ↑ D. Bohm, The Special Theory of Relativity (Benjamin, New York, 1965).
- ↑ W. Heisenberg, Z. Phys. 43, 172 (1927). For an English translation, see Quantum Theory and Measurement ed. J. A. Wheeler and W. H. Zurek (Princeton Univ. Press, New Jersey, 1983), pp. 62-84.
- ↑ D. Bohm, The Special Theory of Relativity (Benjamin, New York, 1965), p. 40.
- ↑ D. Bohm, Phys. Rev. 85, 166 (1952).
- ↑ Q. B. Zheng and T. Kobayashi, Physics Essays 9, 447 (1996).
- ↑ C. F. von Weizsäcker and Th. Görnitz, in Symposium on the foundations of Modern Physics 1993 ed. P. Busch, P. Lahti, and P. Mittelstaedt (World Scientific, Singapore, 1993).
- ↑ R. J. Glauber, Phys. Rev. 130, 2529-2539 (1963).
- ↑ R. J. Glauber, Phys. Rev. 130, 2531 (1963).
- ↑ M. Born, Z. Phys. 37, 863 (1926). For an English translation, see Quantum Theory and Measurement ed. J. A. Wheeler and W. H. Zurek, Princeton Univ. Press, New Jersey, 1983, pp. 52-55.
- ↑ D. Bohm, The Special Theory of Relativity (Benjamin, New York, 1965), p. 52.
- ↑ To emphasize the vast difference in this conceptual framework, the discussion proceeds in contrast with the standard interpretation of the uncertainty relation; see, for example, C. Cohen-Tannoudji, B. Diu, and F. Laloë, Quantum Mechanics Vol. 1, (Wiley, New York, 1977), pp. 21-31.
- ↑ M. Jammer, The Philosophy of Quantum Mechanics, (Wiley, New York, 1974); J. A. Wheeler and W. H. Zurek, Quantum Theory and Measurement, (Princeton Univ. Press, New Jersey, 1983).
- ↑ D. Bohm, The Special Theory of Relativity (Benjamin, New York, 1965), p. 173.
- ↑ D. Bohm, The Special Theory of Relativity (Benjamin, New York, 1965), p. 182.
Further reading
- Zheng, Q.; Kobayashi, T. (1996), "Quantum Optics as a Relativistic Theory of Light", Physics Essays 9: 447, Bibcode:1996PhyEs...9..447Z, doi:10.4006/1.3029255. Annual Report, Department of Physics, School of Science, University of Tokyo (1992) 240.
- S. Kochen, Symposium of the Foundations of Modern Physics: 50 Years of the Einstein-Podolsky-Rosen Gedankenexperiment, (World Scientific Publishing Co., Singapore, 1985), pp. 151–69.
- H. Everett, Rev. of Modern Phys. 29, 454 (1957).
- G. Bene, Physica, A242, 529 (1992).
- S. Kochen, The interpretation of quantum mechanics, (Preprint, Princeton Univ., 1979).
- L. Smolin, The Bekenstein bound, topological quantum field theory and pluralistic quantum field theory, (Preprint, Penn State, 1995).
- C. Rovelli, Int. J. of Theor. Phys. 35, 1637 (1996).
See also
|
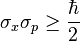
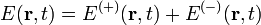
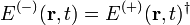
![E^{(+)}(\mathbf {r}, t) = i\sum_{i}[\frac{\hbar\omega_{i}}{2}]^{1/2}\hat{a}_{i}\mathbf{\varepsilon}_{i}e^{i(\mathbf {k}_{i}\cdot\mathbf {r} - \omega_{i}t)}](../I/m/8b758b8735ed372594f29d4082357280.png)