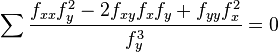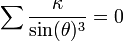Reiss relation

In algebraic geometry, the Reiss relation, introduced by Reiss (1837), is a condition on the second-order elements of the points of a plane algebraic curve meeting a given line.

Statement

If C is a complex plane curve given by the zeros of a polynomial f(x,y) of two variables, and L is a line meeting C transversely and not meeting C at infinity, then

\sum\frac{f_{xx}f_y^2-2f_{xy}f_xf_y+f_{yy}f_x^2}{f_y^3}=0

where the sum is over the points of intersection of C and L, and f_x, f_xy and so on stand for partial derivatives of f (Griffiths & Harris 1994, p. 675). This can also be written as

\sum\frac{\kappa}{\sin(\theta)^3}=0

where κ is the curvature of the curve C and θ is the angle its tangent line makes with L, and the sum is again over the points of intersection of C and L (Griffiths & Harris 1994, p. 677).

References

Griffiths, Phillip; Harris, Joseph (1994), Principles of algebraic geometry, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-05059-9, MR 1288523
Segre, Beniamino (1971), Some properties of differentiable varieties and transformations: with special reference to the analytic and algebraic cases, Ergebnisse der Mathematik und ihrer Grenzgebiete 13, Berlin, New York: Springer-Verlag, ISBN 978-3-540-05085-8, MR 0278222
Akivis, M. A.; Goldberg, V. V.: Projective differential geometry of submanifolds. North-Holland Mathematical Library, 49. North-Holland Publishing Co., Amsterdam, 1993 (chapter 8).