Regularization (mathematics)
Regularization, in mathematics and statistics and particularly in the fields of machine learning and inverse problems, refers to a process of introducing additional information in order to solve an ill-posed problem or to prevent overfitting. This information is usually of the form of a penalty for complexity, such as restrictions for smoothness or bounds on the vector space norm.
A theoretical justification for regularization is that it attempts to impose Occam's razor on the solution. From a Bayesian point of view, many regularization techniques correspond to imposing certain prior distributions on model parameters.
The same idea arose in many fields of science. For example, the least-squares method can be viewed as a very simple form of regularization. A simple form of regularization applied to integral equations, generally termed Tikhonov regularization after Andrey Nikolayevich Tikhonov, is essentially a trade-off between fitting the data and reducing a norm of the solution. More recently, non-linear regularization methods, including total variation regularization have become popular.
Regularization in statistics and machine learning
In statistics and machine learning, regularization methods are used for model selection, in particular to prevent overfitting by penalizing models with extreme parameter values. The most common variants in machine learning are L₁ and L₂ regularization, which can be added to learning algorithms that minimize a loss function E(X, Y) by instead minimizing E(X, Y) + α‖w‖, where w is the model's weight vector, ‖·‖ is either the L₁ norm or the squared L₂ norm, and α is a free parameter that needs to be tuned empirically (typically by cross-validation; see hyperparameter optimization). This method applies to many models. When applied in linear regression, the resulting models are termed ridge regression or lasso, but regularization is also employed in (binary and multiclass) logistic regression, neural nets, support vector machines, conditional random fields and some matrix decomposition methods. L₂ regularization may also be called "weight decay", in particular in the setting of neural nets.
L₁ regularization is often preferred because it produces sparse models and thus performs feature selection within the learning algorithm, but since the L₁ norm is not differentiable, it may require changes to learning algorithms, in particular gradient-based learners.[1][2]
Bayesian learning methods make use of a prior probability that (usually) gives lower probability to more complex models. Well-known model selection techniques include the Akaike information criterion (AIC), minimum description length (MDL), and the Bayesian information criterion (BIC). Alternative methods of controlling overfitting not involving regularization include cross-validation.
Regularization can be used to fine tune model complexity using an augmented error function with cross-validation. The data sets used in complex models can produce a levelling-off of validation as complexity of the models increases. Training data sets errors decrease while the validation data set error remains constant. Regularization introduces a second factor which weights the penalty against more complex models with an increasing variance in the data errors. This gives an increasing penalty as model complexity increases.[3]
Examples of applications of different methods of regularization to the linear model are:
| Model | Fit measure | Entropy measure[4][5] |
|---|---|---|
| AIC/BIC | 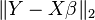 | 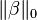 |
| Ridge regression | 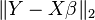 | 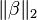 |
| Lasso[6] | 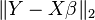 | 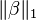 |
| Basis pursuit denoising | 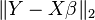 | 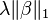 |
| Rudin-Osher-Fatemi model (TV) | 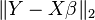 | 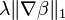 |
| Potts model | 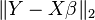 | 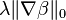 |
| RLAD[7] | 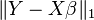 | 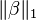 |
| Dantzig Selector[8] | 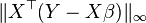 | 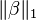 |
| SLOPE[9] | 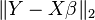 | 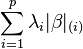 |
A linear combination of the LASSO and ridge regression methods is elastic net regularization.
See also
Notes
- ↑ Andrew, Galen; Gao, Jianfeng (2007). "Scalable training of L₁-regularized log-linear models". Proceedings of the 24th International Conference on Machine Learning. doi:10.1145/1273496.1273501. ISBN 9781595937933.
- ↑ Tsuruoka, Y.; Tsujii, J.; Ananiadou, S. (2009). Stochastic gradient descent training for l1-regularized log-linear models with cumulative penalty. Proceedings of the AFNLP/ACL.
- ↑ Alpaydin, Ethem (2004). Introduction to machine learning. Cambridge, Mass. [u.a.]: MIT Press. pp. 79, 80. ISBN 978-0-262-01211-9. Retrieved 9 March 2011.
- ↑ Bishop, Christopher M. (2007). Pattern recognition and machine learning (Corr. printing. ed.). New York: Springer. ISBN 978-0387310732.
- ↑ Duda, Richard O. (2004). Pattern classification + computer manual : hardcover set (2. ed. ed.). New York [u.a.]: Wiley. ISBN 978-0471703501.
- ↑ Tibshirani, Robert (1996). "Regression Shrinkage and Selection via the Lasso" (PostScript). Journal of the Royal Statistical Society, Series B 58 (1): 267–288. MR 1379242. Retrieved 2009-03-19.
- ↑ Li Wang, Michael D. Gordon & Ji Zhu (2006). "Regularized Least Absolute Deviations Regression and an Efficient Algorithm for Parameter Tuning". Sixth International Conference on Data Mining. pp. 690–700. doi:10.1109/ICDM.2006.134.
- ↑ Candes, Emmanuel; Tao, Terence (2007). "The Dantzig selector: Statistical estimation when p is much larger than n". Annals of Statistics 35 (6): 2313–2351. arXiv:math/0506081. doi:10.1214/009053606000001523. MR 2382644.
- ↑ Małgorzata Bogdan, Ewout van den Berg, Weijie Su & Emmanuel J. Candes (2013). "Statistical estimation and testing via the ordered L1 norm". arXiv preprint arXiv:1310.1969. arXiv:1310.1969v2.
References
- A. Neumaier, Solving ill-conditioned and singular linear systems: A tutorial on regularization, SIAM Review 40 (1998), 636-666. Available in pdf from author's website.