Regular extension

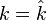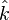In field theory, a branch of algebra, a field extension $L/k$ is said to be regular if k is algebraically closed in L (i.e., $k = \hat k$ where $\hat k$ is the set of elements in L algebraic over k) and L is separable over k, or equivalently, 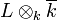$L \otimes_k \overline{k}$ is an integral domain when 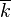$\overline{k}$ is the algebraic closure of 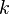$k$ (that is, to say, 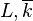$L, \overline{k}$ are linearly disjoint over k).^[1]^[2]

Properties

Regularity is transitive: if F/E and E/K are regular then so is F/K.^[3]
If F/K is regular then so is E/K for any E between F and K.^[3]
The extension L/k is regular if and only if every subfield of L finitely generated over k is regular over k.^[2]
Any extension of an algebraically closed field is regular.^[3]^[4]
An extension is regular if and only if it is separable and primary.^[5]
A purely transcendental extension of a field is regular.

Self-regular extension

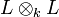There is also a similar notion: a field extension $L / k$ is said to be self-regular if $L \otimes_k L$ is an integral domain. A self-regular extension is relatively algebraically closed in k.^[6] However, a self-regular extension is not necessarily regular.

References

↑ Fried & Jarden (2008) p.38
↑ 2.0 2.1 Cohn (2003) p.425
↑ 3.0 3.1 3.2 Fried & Jarden (2008) p.39
↑ Cohn (2003) p.426
↑ Fried & Jarden (2008) p.44
↑ Cohn (2003) p.427

Fried, Michael D.; Jarden, Moshe (2008). Field arithmetic. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge 11 (3rd revised ed.). Springer-Verlag. pp. 38–41. ISBN 978-3-540-77269-9. Zbl 1145.12001.
M. Nagata (1985). Commutative field theory: new edition, Shokado. (Japanese)
Cohn, P. M. (2003). Basic Algebra. Groups, Rings, and Fields. Springer-Verlag. ISBN 1-85233-587-4. Zbl 1003.00001.
A. Weil, Foundations of algebraic geometry.