Reflective subcategory

In mathematics, a full subcategory A of a category B is said to be reflective in B when the inclusion functor from A to B has a left adjoint. This adjoint is sometimes called a reflector. Dually, A is said to be coreflective in B when the inclusion functor has a right adjoint.

Informally, a reflector acts as a kind of completion operation. It adds in any "missing" pieces of the structure in such a way that reflecting it again has no further effect.

Definition

A full subcategory A of a category B is said to be reflective in B if for each B-object B there exists an A-object 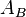$A_B$ and a B-morphism 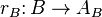$r_B \colon B \to A_B$ such that for each B-morphism 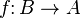$f\colon B\to A$ there exists a unique A-morphism $\overline f \colon A_B \to A$ with $\overline f\circ r_B=f$ .

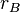The pair $(A_B,r_B)$ is called the A-reflection of B. The morphism $r_B$ is called A-reflection arrow. (Although often, for the sake of brevity, we speak about 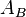$A_B$ only as about the A-reflection of B).

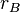This is equivalent to saying that the embedding functor $E\colon \mathbf{A} \hookrightarrow \mathbf{B}$ is adjoint. The coadjoint functor $R \colon \mathbf B \to \mathbf A$ is called the reflector. The map $r_B$ is the unit of this adjunction.

The reflector assigns to $B$ the A-object 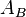$A_B$ and $Rf$ for a B-morphism $f$ is determined by the commuting diagram

If all A-reflection arrows are (extremal) epimorphisms, then the subcategory A is said to be (extremal) epireflective. Similarly, it is bireflective if all reflection arrows are bimorphisms.

All these notions are special case of the common generalization — $E$ -reflective subcategory, where $E$ is a class of morphisms.

The $E$ -reflective hull of a class A of objects is defined as the smallest $E$ -reflective subcategory containing A. Thus we can speak about reflective hull, epireflective hull, extremal epireflective hull, etc.

Dual notions to the above mentioned notions are coreflection, coreflection arrow, (mono)coreflective subcategory, coreflective hull.

Examples

Algebra

The category of abelian groups Ab is a reflective subcategory of the category of groups, Grp. The reflector is the functor which sends each group to its abelianization. In its turn, the category of groups is a reflective subcategory of the category of inverse semigroups.^[1]
Similarly, the category of commutative associative algebras is a reflective subcategory of all associative algebras, where the reflector is quotienting out by the commutator ideal. This is used in the construction of the symmetric algebra from the tensor algebra.
Dually, the category of anti-commutative associative algebras is a reflective subcategory of all associative algebras, where the reflector is quotienting out by the anti-commutator ideal. This is used in the construction of the exterior algebra from the tensor algebra.
The category of fields is a reflective subcategory of the category of integral domains (with injective ring homomorphisms as morphisms). The reflector is the functor which sends each integral domain to its field of fractions.
The category of abelian torsion groups is a coreflective subcategory of the category of abelian groups. The coreflector is the functor sending each group to its torsion subgroup.
The categories of elementary abelian groups, abelian p-groups, and p-groups are all reflective subcategories of the category of groups, and the kernels of the reflection maps are important objects of study; see focal subgroup theorem.

Topology

Kolmogorov spaces (T₀ spaces) are a reflective subcategory of Top, the category of topological spaces, and the Kolmogorov quotient is the reflector.
The category of completely regular spaces CReg is a reflective subcategory of Top. By taking Kolmogorov quotients, one sees that the subcategory of Tychonoff spaces is also reflective.
The category of all compact Hausdorff spaces is a reflective subcategory of the category of all Tychonoff spaces. The reflector is given by the Stone–Čech compactification.
The category of all complete metric spaces with uniformly continuous mappings is a reflective subcategory of the category of metric spaces. The reflector is the completion of a metric space on objects, and the extension by density on arrows.

Functional analysis

The category of Banach spaces is a reflective subcategory of the category of normed spaces and bounded linear operators. The reflector is the norm completion functor.

Category theory

For any Grothendieck site (C,J), the topos of sheaves on (C,J) is a reflective subcategory of the topos of presheaves on C, with the special further property that the reflector functor is left exact. The reflector is the sheafification functor a: Presh(C) → Sh(C,J), and the adjoint pair (a,i) is an important example of a geometric morphism in topos theory.

Notes

↑ Lawson (1998), p. 63, Theorem 2.

References

Adámek, Jiří; Horst Herrlich; George E. Strecker (1990). Abstract and Concrete Categories. New York: John Wiley & Sons.
Peter Freyd, Andre Scedrov (1990). Categories, Allegories. Mathematical Library Vol 39. North-Holland. ISBN 978-0-444-70368-2.
Herrlich, Horst (1968). Topologische Reflexionen und Coreflexionen. Lecture Notes in Math. 78. Berlin: Springer.
Mark V. Lawson (1998). Inverse semigroups: the theory of partial symmetries. World Scientific. ISBN 978-981-02-3316-7.