Rees algebra
In commutative algebra, the Rees algebra of an ideal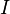 
in a ring 
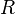is defined to be
![\oplus_{n=0}^{\infty} I^n t^n=R[It]\subset R[t].](../I/m/d97d55eaa4a17ba77d93d3e3ac4af91b.png)
This construction has special interest in algebraic geometry since the projective scheme defined by the Rees algebra of an ideal in a ring is the blowing-up of the spectrum of the ring along the subscheme defined by the ideal.[1]
The associated graded ring of a Rees algebra of an ideal I is called (slightly abusively) the special fiber and the Krull dimension of the special fiber is called the analytic spread of I.
References
- ↑ Eisenbud-Harris, The geometry of schemes. Springer-Verlag, 197, 2000
External links
- What Is the Rees Algebra of a Module?
- http://mathoverflow.net/questions/143746/geometry-behind-rees-algebra-deformation-to-the-normal-cone?rq=1