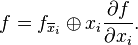Reed–Muller expansion
In Boolean logic, a Reed–Muller (or Davio) expansion is a decomposition of a boolean function.
For a boolean function 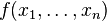 we set with respect to
we set with respect to 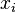 :
:
as the positive and negative cofactors of  , and the boolean derivation of
, and the boolean derivation of  .
.
Then we have for the Reed–Muller or positive Davio expansion:
Similar to binary decision diagrams (BDDs), where nodes represent Shannon expansion with respect to the according variable, we can define a decision diagram based on the Reed–Muller expansion. These decision diagrams are called functional BDDs (FBDDs).
References
- Kebschull, U. and Rosenstiel, W., Efficient graph-based computation and manipulation of functional decision diagrams, Proceedings 4th European Conference on Design Automation, 1993, pp. 278–282
![\begin{align}
f_{{x_i}}(x) & = f(x_1,\ldots,x_{i-1},1,x_{i+1},\ldots,x_n) \\[3pt]
f_{\overline{x}_i}(x)& = f(x_1,\ldots,x_{i-1},0,x_{i+1},\ldots,x_n) \\[3pt]
\frac{\partial f}{\partial x_i} & = f_{x_i}(x) \oplus f_{\overline{x}_i}(x)\, \\
\end{align}](../I/m/7491b8172fdfd2619121163fc8406304.png)