Reduced residue system
Any subset R of the integers is called a reduced residue system modulo n if
- gcd(r, n) = 1 for each r contained in R;
- R contains φ(n) elements;
- no two elements of R are congruent modulo n.[1][2]
Here 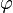 denotes Euler's totient function.
denotes Euler's totient function.
A reduced residue system modulo n can be formed from a complete residue system modulo n by removing all integers not relatively prime to n. For example, a complete residue system modulo 12 is {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}. 1, 5, 7 and 11 are the only integers in this set which are relatively prime to 12, and so the corresponding reduced residue system modulo 12 is {1,5,7,11}. The cardinality of this set can be calculated with the totient function: 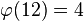 . Some other reduced residue systems modulo 12 are:
. Some other reduced residue systems modulo 12 are:
- {13,17,19,23}
- {−11,−7,−5,−1}
- {−7,−13,13,31}
- {35,43,53,61}
Facts
- If {r1, r2, ... , rφ(n)} is a reduced residue system with n > 2, then
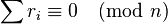 .
. - Every number in a reduced residue system mod n is a generator for the additive group of integers modulo n.
See also
- Complete residue system modulo m
- Congruence relation
- Euler's totient function
- Greatest common divisor
- Least residue system modulo m
- Modular arithmetic
- Number theory
- Residue number system
Notes
- ↑ Long (1972, p. 85)
- ↑ Pettofrezzo & Byrkit (1970, p. 104)
References
- Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: D. C. Heath and Company, LCCN 77171950
- Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 71081766
External links
- Residue systems at PlanetMath
- Reduced residue system at MathWorld