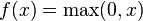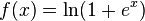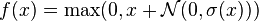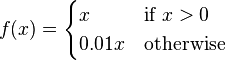Rectifier (neural networks)

Plot of the rectifier (blue) and softplus (green) functions near

x

= 0.

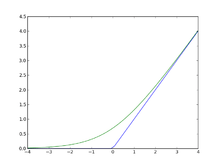
In the context of artificial neural networks, the rectifier is an activation function defined as

f(x) = \max(0, x)

where x is the input to a neuron. This activation function has been argued to be more biologically plausible (cortical neurons are rarely in their maximum saturation regime) ^[1] than the widely used logistic sigmoid (which is inspired by probability theory; see logistic regression) and its more practical^[2] counterpart, the hyperbolic tangent.

A unit employing the rectifier is also called a rectified linear unit (ReLU).^[3]

A smooth approximation to the rectifier is the analytic function

f(x) = \ln(1 + e^x)

which is called the softplus function.^[4] The derivative of softplus is 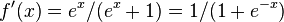$f'(x) = e^x / (e^x+1) = 1 / (1 + e^{-x})$ , i.e. the logistic function.

Rectified linear units find applications in computer vision using deep neural nets.^[1]

Variants

Noisy ReLUs

Rectified linear units can be extended to include Gaussian noise, making them noisy ReLUs, giving^[3]

f(x) = \max(0, x + \mathcal{N}(0, \sigma(x)))

Noisy ReLUs have been used with some success in restricted Boltzmann machines for computer vision tasks.^[3]

Leaky ReLUs

Leaky ReLUs allow a small, non-zero gradient when the unit is not active.^[5]

f(x) = \begin{cases} x & \mbox{if } x > 0 \\ 0.01x & \mbox{otherwise} \end{cases}

Advantages

Biological plausibility: One-sided, compared to the antisymmetry of tanh.
Sparse activation: For example, in a randomly initialized networks, only about 50% of hidden units are activated (having a non-zero output).
Efficient gradient propagation: No vanishing gradient problem or exploding effect.
Efficient computation: Only comparison, addition and multiplication.

Rectified linear units, compared to sigmoid function or similar activation functions, allow for faster and effective training of deep neural architectures on large and complex datasets. The common trait is that they implement local competition between small groups of units within a layer (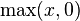 $\max(x,0)$ can be interpreted as competition with a fixed value of 0), so that only part of the network is activated for any given input pattern.^[6]

Potential problems

Identifiability: There are infinitely many ways of setting values to parameters of a rectifier network to express an overall network function.^[1]^:319
Non-differentiable at zero: however it is differentiable at any point arbitrarily close to 0.

Also see

References

↑ 1.0 1.1 1.2 Xavier Glorot, Antoine Bordes and Yoshua Bengio (2011). Deep sparse rectifier neural networks (PDF). AISTATS.
↑ Yann LeCun, Leon Bottou, Genevieve B. Orr and Klaus-Robert Müller (1998). "Efficient BackProp" (PDF). In G. Orr and K. Müller. Neural Networks: Tricks of the Trade. Springer.
↑ 3.0 3.1 3.2 Vinod Nair and Geoffrey Hinton (2010). Rectified linear units improve restricted Boltzmann machines (PDF). ICML.
↑ F. Bélisle, Y. Bengio, C. Dugas, R. Garcia, C. Nadeau (2001). Second-Order Functional Knowledge for Better Option Pricing
↑ Andrew L. Maas, Awni Y. Hannun, Andrew Y. Ng (2014). Rectifier Nonlinearities Improve Neural Network Acoustic Models
↑ RK Srivastava, J Masci,F Gomez, and J Schmidhuber (2014). Understanding Locally Competitive Networks (PDF). arXiv.