Realcompact space

In mathematics, in the field of topology, a topological space is said to be realcompact if it is completely regular Hausdorff and every point of its Stone–Čech compactification is real (meaning that the quotient field at that point of the ring of real functions is the reals). Realcompact spaces have also been called Q-spaces, saturated spaces, functionally complete spaces, real-complete spaces, replete spaces and Hewitt-Nachbin spaces (named after Edwin Hewitt and Leopoldo Nachbin). Realcompact spaces were introduced by Hewitt (1948).

Properties

• A space is realcompact if and only if it can be embedded homeomorphically as a closed subset in some (not necessarily finite) Cartesian power of the reals, with the product topology. Moreover, a (Hausdorff) space is realcompact if and only if it has the uniform topology and is complete for the uniform structure generated by the continuous real-valued functions (Gillman, Jerison, p. 226).

• For example Lindelöf spaces are realcompact; in particular all subsets of 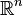are realcompact.

• The (Hewitt) realcompactification υX of a topological space X consists of the real points of its Stone–Čech compactification βX. A topological space X is realcompact if and only if it coincides with its Hewitt realcompactification.

• Write C(X) for the ring of continuous functions on a topological space X. If Y is a real compact space, then ring homomorphisms from C(Y) to C(X) correspond to continuous maps from X to Y. In particular the category of realcompact spaces is dual to the category of rings of the form C(X).

• In order that a Hausdorff space X is compact it is necessary and sufficient that X is realcompact and pseudocompact (see Engelking, p. 153).

See also

• Compact space
• Paracompact space
• Normal space
• Pseudocompact space
• Tychonoff space

References

• Gillman, Leonard; Jerison, Meyer, "Rings of continuous functions". Reprint of the 1960 edition. Graduate Texts in Mathematics, No. 43. Springer-Verlag, New York-Heidelberg, 1976. xiii+300 pp.
• Hewitt, Edwin (1948), "Rings of real-valued continuous functions. I", Transactions of the American Mathematical Society 64: 45–99, ISSN 0002-9947, JSTOR 1990558, MR 0026239 .
• Engelking, Ryszard (1968). Outline of General Topology. translated from Polish. Amsterdam: North-Holland Publ. Co. .
• Willard, Stephen (1970), General Topology, Reading, Mass.: Addison-Wesley .