Real tree
In mathematics, a real tree, or an 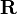 -tree, is a metric space (M,d) such that
for any x, y in M there is a unique arc from x to y. Here by an arc from x to y we mean the image in M of a topological embedding f from an interval [a,b] to M such that f(a)=x and f(b)=y (for some real numbers a and b). Note that uniqueness refers to the image in M.
Moreover, by choosing a and b so that d(x, y)=|a-b| and using arclength parametrization for the interval [a, b], we may assume that this arc is a geodesic segment. The condition that the arc is a geodesic segment means that the map f above is an isometric embedding, that is, for every z, t in [a,b] we have d(f(z), f(t))=|z-t|.
-tree, is a metric space (M,d) such that
for any x, y in M there is a unique arc from x to y. Here by an arc from x to y we mean the image in M of a topological embedding f from an interval [a,b] to M such that f(a)=x and f(b)=y (for some real numbers a and b). Note that uniqueness refers to the image in M.
Moreover, by choosing a and b so that d(x, y)=|a-b| and using arclength parametrization for the interval [a, b], we may assume that this arc is a geodesic segment. The condition that the arc is a geodesic segment means that the map f above is an isometric embedding, that is, for every z, t in [a,b] we have d(f(z), f(t))=|z-t|.
Equivalently, a geodesic metric space M is a real tree if and only if M is a δ-hyperbolic space with δ=0.
Complete real trees are injective metric spaces (Kirk 1998).
There is a theory of group actions on R-trees, known as the Rips machine, which is part of geometric group theory.
Simplicial R-trees
A simplicial R-tree is an R-tree that is free from certain "topological strangeness". More precisely, a point x in an R-tree T is called ordinary if T−x has exactly two components. The points which are not ordinary are singular. We define a simplicial R-tree to be an R-tree whose set of singular points is discrete and closed.
Examples
- Each discrete tree can be regarded as an R-tree by a simple construction such that neighboring vertices have distance one.
- The Paris metric makes the plane into an R-tree. If two points are on the same ray in the plane, their distance is defined as the Euclidean distance. Otherwise, their distance is defined to be the sum of the Euclidean distances of these two points to the origin. More generally any hedgehog space is an example of a real tree.
- The R-tree obtained in the following way is nonsimplicial. Start with the interval [0,2] and glue, for each positive integer n, an interval of length 1/n to the point 1−1/n in the original interval. The set of singular points is discrete, but fails to be closed since 1 is an ordinary point in this R-tree. Gluing an interval to 1 would result in a closed set of singular points at the expense of discreteness.
See also
References
- Bestvina, Mladen (2002), "ℝ-trees in topology, geometry, and group theory", Handbook of geometric topology, Amsterdam: North-Holland, pp. 55–91, MR 1886668.
- Chiswell, Ian (2001), Introduction to Λ-trees, River Edge, NJ: World Scientific Publishing Co. Inc., ISBN 981-02-4386-3, MR 1851337.
- Kirk, W. A. (1998), "Hyperconvexity of R-trees", Fundamenta Mathematicae 156 (1): 67–72, MR 1610559.
- Shalen, Peter B. (1987), "Dendrology of groups: an introduction", in Gersten, S. M., Essays in group theory, Math. Sci. Res. Inst. Publ. 8, Springer-Verlag, pp. 265–319, ISBN 978-0-387-96618-2, MR 919830.