Read-only right moving Turing machines
Read-only right moving Turing machines are a particular type of Turing machine.
Definition
The definition based on a single infinite tape defined to be a 7-tuple
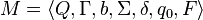where
-
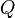is a finite set of states -
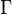is a finite set of the tape alphabet/symbols -
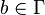is the blank symbol (the only symbol allowed to occur on the tape infinitely often at any step during the computation) -
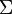, a subset of 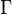not including b is the set of input symbols -
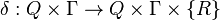is a function called the transition function, R is a right movement (a right shift). -
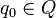is the initial state -
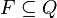is the set of final or accepting states
In the case of these types of Turing Machines, the only movement is to the right.
There must exist at least one element of the set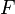 
(a HALT state) for the machine to accept a regular language (Not in including the empty language).
An example Read Only right moving Turing machine
- Q = { A, B, C, HALT }
- Γ = { 0, 1 }
- b = 0 = "blank"
- Σ =
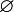, empty set - δ = see state-table below
- q0 = A = initial state
- F = the one element set of final states {HALT}
State table for 3 state, 2 symbol read only machine:
| Current state A: | Current state B: | Current state C: | |||||||
| Write symbol: | Move tape: | Next state: | Write symbol: | Move tape: | Next state: | Write symbol: | Move tape: | Next state: | |
| tape symbol is 0: | 1 | R | B | 1 | R | A | 1 | R | B |
| tape symbol is 1: | 1 | R | C | 1 | R | B | 1 | N | HALT |
See also
- DFA
- NFA
- Finite State Machine
- Read-only Turing machine
- Turing Machine
- Turing machine examples
References
- Davis, Martin; Ron Sigal; Elaine J. Weyuker (1994). Second Edition: Computability, Complexity, and Languages and Logic: Fundamentals of Theoretical Computer Science (2nd ed. ed.). San Diego: Academic Press, Harcourt, Brace & Company. ISBN 0-12-206382-1.