Reaching definition
In compiler theory, a reaching definition for a given instruction is an earlier instruction whose target variable can reach the given one without an intervening assignment. For example, in the following code:
d1 : y := 3 d2 : x := y
d1 is a reaching definition for d2. In the following, example, however:
d1 : y := 3 d2 : y := 4 d3 : x := y
d1 is no longer a reaching definition for d3, because d2 kills its reach.
As analysis
The similarly named reaching definitions is a data-flow analysis which statically determines which definitions may reach a given point in the code. Because of its simplicity, it is often used as the canonical example of a data-flow analysis in textbooks. The data-flow confluence operator used is set union, and the analysis is forward flow. Reaching definitions are used to compute use-def chains and def-use chains.
The data-flow equations used for a given basic block 
in reaching definitions are:
![{\rm REACH}_{\rm in}[S] = \bigcup_{p \in pred[S]} {\rm REACH}_{\rm out}[p]](../I/m/8d2af47bafb16979087feca8334e19e3.png)
![{\rm REACH}_{\rm out}[S] = {\rm GEN}[S] \cup ({\rm REACH}_{\rm in}[S] - {\rm KILL}[S])](../I/m/3823ab95c263771469e5578ac3bcc99c.png)
In other words, the set of reaching definitions going into are all of the reaching definitions from 's predecessors, ![pred[S]](../I/m/74fa0cc8099dbf9ae72051efe2c2f2f3.png)
. consists of all of the basic blocks that come before in the control flow graph. The reaching definitions coming out of are all reaching definitions of its predecessors minus those reaching definitions whose variable is killed by plus any new definitions generated within .
For a generic instruction, we define the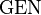 
and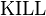 
sets as follows:
![{\rm GEN}[d : y \leftarrow f(x_1,\cdots,x_n)] = \{d\}](../I/m/0df023e3b86c649375f12587b849d8f3.png)
![{\rm KILL}[d : y \leftarrow f(x_1,\cdots,x_n)] = {\rm DEFS}[y] - \{d\}](../I/m/f462f7e86e80e96e3432e4fa23fd4529.png)
where ![{\rm DEFS}[y]](../I/m/b0acfa394238bd0008ec251e8e4fc196.png)
is the set of all definitions that assign to the variable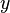 
. Here 
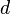is a unique label attached to the assigning instruction; thus, the domain of values in reaching definitions are these instruction labels.
Further reading
- Aho, Alfred V.; Sethi, Ravi; & Ullman, Jeffrey D. (1986). Compilers: Principles, Techniques, and Tools. Addison Wesley. ISBN 0-201-10088-6.
- Appel, Andrew W. (1999). Modern Compiler Implementation in ML. Cambridge University Press. ISBN 0-521-58274-1.
- Cooper, Keith D.; & Torczon, Linda. (2005). Engineering a Compiler. Morgan Kaufmann. ISBN 1-55860-698-X.
- Muchnick, Steven S. (1997). Advanced Compiler Design and Implementation. Morgan Kaufmann. ISBN 1-55860-320-4.
- Nielson F., H.R. Nielson;, C. Hankin (2005). Principles of Program Analysis. Springer. ISBN 3-540-65410-0.