Rayleigh quotient
In mathematics, for a given complex Hermitian matrix M and nonzero vector x, the Rayleigh quotient[1]  , is defined as:[2][3]
, is defined as:[2][3]
For real matrices and vectors, the condition of being Hermitian reduces to that of being symmetric, and the conjugate transpose 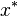 to the usual transpose
to the usual transpose 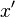 . Note that
. Note that  for any non-zero real scalar c. Recall that a Hermitian (or real symmetric) matrix has real eigenvalues. It can be shown that, for a given matrix, the Rayleigh quotient reaches its minimum value
for any non-zero real scalar c. Recall that a Hermitian (or real symmetric) matrix has real eigenvalues. It can be shown that, for a given matrix, the Rayleigh quotient reaches its minimum value 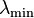 (the smallest eigenvalue of M) when x is
(the smallest eigenvalue of M) when x is 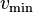 (the corresponding eigenvector). Similarly,
(the corresponding eigenvector). Similarly, 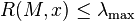 and
and 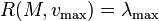 .
.
The Rayleigh quotient is used in the min-max theorem to get exact values of all eigenvalues. It is also used in eigenvalue algorithms to obtain an eigenvalue approximation from an eigenvector approximation. Specifically, this is the basis for Rayleigh quotient iteration.
The range of the Rayleigh quotient (for matrix that is not necessarily Hermitian) is called a numerical range, (or spectrum in functional analysis). When the matrix is Hermitian, the
numerical range is equal to the spectral norm. Still in functional analysis, 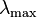 is known as the spectral radius. In the context of C*-algebras or algebraic quantum mechanics, the function that to M associates the Rayleigh-Ritz quotient R(M,x) for a fixed x and M varying through the algebra would be referred to as "vector state" of the algebra.
is known as the spectral radius. In the context of C*-algebras or algebraic quantum mechanics, the function that to M associates the Rayleigh-Ritz quotient R(M,x) for a fixed x and M varying through the algebra would be referred to as "vector state" of the algebra.
Bounds for Hermitian 
As stated in introduction ![R(M,x) \in \left[\lambda_\min, \lambda_\max \right]](../I/m/b8a49cf38b2683b62850ccbae177f26c.png) . This is immediate after observing that the Rayleigh quotient is a weighted average of eigenvalues of M:
. This is immediate after observing that the Rayleigh quotient is a weighted average of eigenvalues of M:
where 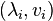 is the
is the  th eigenpair after orthonormalization and
th eigenpair after orthonormalization and 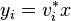 is the
is the  th coordinate of x in the eigenbasis. It is then easy to verify that the bounds are attained at the corresponding eigenvectors
th coordinate of x in the eigenbasis. It is then easy to verify that the bounds are attained at the corresponding eigenvectors 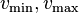 .
.
The fact that the quotient is a weighted average of the eigenvalues can be used to identify the second, the third, ... largest eigenvalues. Let 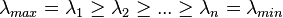 be the eigenvalues in decreasing order. If
be the eigenvalues in decreasing order. If  is constrained to be orthogonal to
is constrained to be orthogonal to 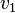 , in which case
, in which case  , then
, then  has the maximum
has the maximum 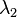 , which is achieved when
, which is achieved when 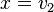 .
.
Special case of covariance matrices
An empirical covariance matrix M can be represented as the product A' A of the data matrix A pre-multiplied by its transpose A'. Being a positive semi-definite matrix, M has non-negative eigenvalues, and orthogonal (or othogonalisable) eigenvectors, which can be demonstrated as follows.
Firstly, that the eigenvalues 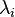 are non-negative:
are non-negative:
Secondly, that the eigenvectors vi are orthogonal to one another:
If the eigenvalues are different – in the case of multiplicity, the basis can be orthogonalized.
To now establish that the Rayleigh quotient is maximised by the eigenvector with the largest eigenvalue, consider decomposing an arbitrary vector x on the basis of the eigenvectors vi:
where
is the coordinate of x orthogonally projected onto vi. Therefore we have:
which, by orthogonality of the eigenvectors, becomes:
The last representation establishes that the Rayleigh quotient is the sum of the squared cosines of the angles formed by the vector x and each eigenvector vi, weighted by corresponding eigenvalues.
If a vector x maximizes  , then any non-zero scalar multiple kx also maximizes R, so the problem can be reduced to the Lagrange problem of maximizing
, then any non-zero scalar multiple kx also maximizes R, so the problem can be reduced to the Lagrange problem of maximizing 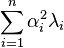 under the constraint that
under the constraint that 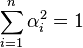 .
.
Define: βi = α2
i. This then becomes a linear program, which always attains its maximum at one of the corners of the domain. A maximum point will have  and
and  for all i > 1 (when the eigenvalues are ordered by decreasing magnitude).
for all i > 1 (when the eigenvalues are ordered by decreasing magnitude).
Thus, as advertised, the Rayleigh quotient is maximised by the eigenvector with the largest eigenvalue.
Formulation using Lagrange multipliers
Alternatively, this result can be arrived at by the method of Lagrange multipliers. The problem is to find the critical points of the function
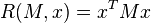 ,
,
subject to the constraint  I.e. to find the critical points of
I.e. to find the critical points of
where λ is a Lagrange multiplier. The stationary points of 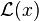 occur at
occur at
and
Therefore, the eigenvectors 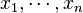 of M are the critical points of the Rayleigh Quotient and their corresponding eigenvalues
of M are the critical points of the Rayleigh Quotient and their corresponding eigenvalues 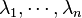 are the stationary values of R.
are the stationary values of R.
This property is the basis for principal components analysis and canonical correlation.
Use in Sturm–Liouville theory
Sturm–Liouville theory concerns the action of the linear operator
on the inner product space defined by
of functions satisfying some specified boundary conditions at a and b. In this case the Rayleigh quotient is
This is sometimes presented in an equivalent form, obtained by separating the integral in the numerator and using integration by parts:
Generalizations
- For a given pair (A, B) of matrices, and a given non-zero vector x, the generalized Rayleigh quotient is defined as:
-
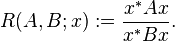
- The Generalized Rayleigh Quotient can be reduced to the Rayleigh Quotient
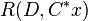 through the transformation
through the transformation  where
where  is the Cholesky decomposition of the Hermitian positive-definite matrix B.
is the Cholesky decomposition of the Hermitian positive-definite matrix B.
- For a given pair (x, y) of non-zero vectors, and a given Hermitian matrix H, the generalized Rayleigh quotient can be defined as:
-
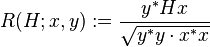
- which coincides with R(H,x) when x=y.
-
See also
- Field of values
- Min-max theorem
References
- ↑ Also known as the Rayleigh–Ritz ratio; named after Walther Ritz and Lord Rayleigh.
- ↑ Horn, R. A. and C. A. Johnson. 1985. Matrix Analysis. Cambridge University Press. pp. 176–180.
- ↑ Parlet B. N. The symmetric eigenvalue problem, SIAM, Classics in Applied Mathematics,1998
Further reading
- Shi Yu, Léon-Charles Tranchevent, Bart Moor, Yves Moreau, Kernel-based Data Fusion for Machine Learning: Methods and Applications in Bioinformatics and Text Mining, Ch. 2, Springer, 2011.
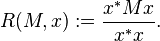
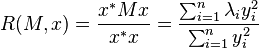
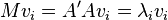

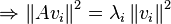
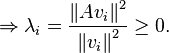
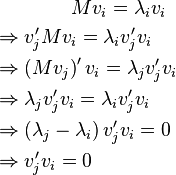
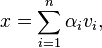
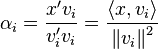

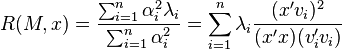


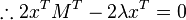
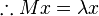

![L(y) = \frac{1}{w(x)}\left(-\frac{d}{dx}\left[p(x)\frac{dy}{dx}\right] + q(x)y\right)](../I/m/f7a279e06daa340e9ecd72639b512b93.png)
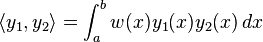
![\frac{\langle{y,Ly}\rangle}{\langle{y,y}\rangle} = \frac{\int_a^b y(x)\left(-\frac{d}{dx}\left[p(x)\frac{dy}{dx}\right] + q(x)y(x)\right)dx}{\int_a^b{w(x)y(x)^2}dx}.](../I/m/92161e3ac0449bd2d27c5925eba06712.png)
![\begin{align}
\frac{\langle{y,Ly}\rangle}{\langle{y,y}\rangle} &= \frac{ \left \{ \int_a^b y(x)\left(-\frac{d}{dx}\left[p(x)y'(x)\right]\right) dx \right \}+ \left \{\int_a^b{q(x)y(x)^2} \, dx \right \}}{\int_a^b{w(x)y(x)^2} \, dx} \\
&= \frac{ \left \{\left. -y(x)\left[p(x)y'(x)\right] \right |_a^b \right \} + \left \{\int_a^b y'(x)\left[p(x)y'(x)\right] \, dx \right \} + \left \{\int_a^b{q(x)y(x)^2} \, dx \right \}}{\int_a^b w(x)y(x)^2 \, dx}\\
&= \frac{ \left \{ \left. -p(x)y(x)y'(x) \right |_a^b \right \} + \left \{ \int_a^b \left [p(x)y'(x)^2 + q(x)y(x)^2 \right] \, dx \right \} } {\int_a^b{w(x)y(x)^2} \, dx}.
\end{align}](../I/m/9956a15f59c5e6d6d7a8ae06e4c30e32.png)