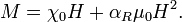Rayleigh law

This article is about the magnetic law. For the stochastic distribution, see Rayleigh distribution. For optical scattering, see Rayleigh scattering. For wireless multipath propagation, see Rayleigh fading.

The Rayleigh law describes the behavior of ferromagnetic materials at low fields.

Ferromagnetic materials consist of magnetic domains. When a small external field 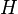H is applied, domains parallel to the external field start to grow. In this region, domain walls are moving. They are hindered by material defects. Lord Rayleigh investigated this first [1] and quantified the magnetization 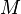M as a linear and quadratic term in the field:

M = \chi_0 H + \alpha_R \mu_0 H^2.

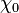Here \chi_0 is the initial susceptibility, describing the reversible part of magnetisation reversal. The Rayleigh constant 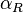\alpha_R describes the irreversible Barkhausen jumps.

The Rayleigh law was derived theoretically by Louis Néel.,[2][3]

The same law describes polarization[4] and direct[5] and converse[6] piezoelectric response of some ferroelectric and ferroelectric-ferroelastic materials. The common feature for ferromagnetic, ferroelectric and ferroelastic materials (i.e., ferroic materials) are domains whose boundaries (domain walls) can be moved by magnetic, electric or mechanical fields.

References

  1. ↑ Rayleigh, Lord (1887). "On the behaviour of iron and steel under the operation of feeble magnetic forces". Phil. Mag. 1 23: 225–248. doi:10.1080/14786448708628000.
  2. ↑ Néel, Louis (1942). "Théories des lois d'aimantation de Lord Rayleigh". Cahiers Phys. 12: 1–20.
  3. ↑ Néel, Louis (1955). "Some theoretical aspects of rock-magnetism". Adv. Phys. 4: 191–243. doi:10.1080/00018735500101204.
  4. ↑ Turik, A.V. (1963). "Theory of polarization and hysteresis of ferroelectrics". Soviet Phys.-Solid State 5 (4): 885–887.
  5. ↑ Damjanovic, D. (1997). "Stress and frequency dependence of the direct piezoelectric effect in ferroelectric ceramics". J. Appl. Phys. 82 (4): 1788–1797.
  6. ↑ Taylor, D.V.; Damjanovic, D.; Setter, N. (1999). "Nonlinear contributions to dielectric and piezoelectric properties in lead zirconate titanate thin films". Ferroelectrics 224 (4): 299–306.