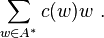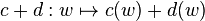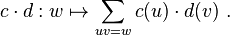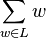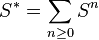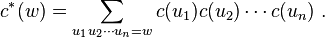Rational series
In mathematics and computer science, a rational series is a generalisation of the concept of formal power series over a ring to the case when the basic algebraic structure is no longer a ring but a semiring, and the indeterminates adjoined are not assumed to commute. They can be regarded as algebraic expressions of a formal language over a finite alphabet.
Definition
Let R be a semiring and A a finite alphabet.
A noncommutative polynomial over A is a finite formal sum of words over A. They form a semiring 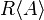 .
.
A formal series is a R-valued function c, on the free monoid A*, which may be written as
The set of formal series is denoted 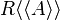 and becomes a semiring under the operations
and becomes a semiring under the operations
A non-commutative polynomial thus corresponds to a function c on A* of finite support.
In the case when R is a ring, then this is the Magnus ring over R.[1]
If L is a language over A, regarded as a subset of A* we can form the characteristic series of L as the formal series
corresponding to the characteristic function of L.
In 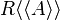 one can define an operation of iteration expressed as
one can define an operation of iteration expressed as
and formalised as
The rational operations are the addition and multiplication of formal series, together with iteration.
A rational series is a formal series obtained by rational operations from 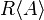 .
.
See also
- Formal power series
- Rational language
- Rational set
- Hahn series (Malcev–Neumann series)
- Weighted automaton
References
- ↑ Koch, Helmut (1997). Algebraic Number Theory. Encycl. Math. Sci. 62 (2nd printing of 1st ed.). Springer-Verlag. p. 167. ISBN 3-540-63003-1. Zbl 0819.11044.
- Berstel, Jean; Reutenauer, Christophe (2011). Noncommutative rational series with applications. Encyclopedia of Mathematics and Its Applications 137. Cambridge: Cambridge University Press. ISBN 978-0-521-19022-0. Zbl 1250.68007.
Further reading
- Sakarovitch, Jacques (2009). Elements of automata theory. Translated from the French by Reuben Thomas. Cambridge: Cambridge University Press. Part IV (where they are called
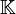 -rational series). ISBN 978-0-521-84425-3. Zbl 1188.68177.
-rational series). ISBN 978-0-521-84425-3. Zbl 1188.68177. - Droste, M., & Kuich, W. (2009). Semirings and Formal Power Series. Handbook of Weighted Automata, 3–28. doi:10.1007/978-3-642-01492-5_1
- Sakarovitch, J. Rational and Recognisable Power Series. Handbook of Weighted Automata, 105–174 (2009). doi:10.1007/978-3-642-01492-5_4
- W. Kuich. Semirings and formal power series: Their relevance to formal languages and automata theory. In G. Rozenberg and A. Salomaa, editors, Handbook of Formal Languages, volume 1, Chapter 9, pages 609–677. Springer, Berlin, 1997