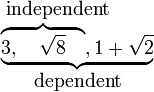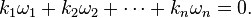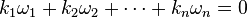Rational dependence

In mathematics, a collection of real numbers is rationally independent if none of them can be written as a linear combination of the other numbers in the collection with rational coefficients. A collection of numbers which is not rationally independent is called rationally dependent. For instance we have the following example.

\begin{matrix} \mbox{independent}\qquad\\ \underbrace{ \overbrace{ 3,\quad \sqrt{8}\quad }, 1+\sqrt{2} }\\ \mbox{dependent}\\ \end{matrix}

Formal definition

The real numbers ω1, ω2, ... , ωn are said to be rationally dependent if there exist integers k1, k2, ... , kn, not all of which are zero, such that

k_1 \omega_1 + k_2 \omega_2 + \cdots + k_n \omega_n = 0.

If such integers do not exist, then the vectors are said to be rationally independent. This condition can be reformulated as follows: ω1, ω2, ... , ωn are rationally independent if the only n-tuple of integers k1, k2, ... , kn such that

k_1 \omega_1 + k_2 \omega_2 + \cdots + k_n \omega_n = 0

is the trivial solution in which every ki is zero.

The real numbers form a vector space over the rational numbers, and this is equivalent to the usual definition of linear independence in this vector space.

See also

Bibliography